PCR/qPCR-Datenanalyse

A Technical Guide to PCR Technologies

• PCR/qPCR Qualitative Analyse
• qPCR Datenanalyse
• Genaue Cq-Werte ermitteln
• Schwellenwert einstellen
• qPCR Quantifizierungsstrategien
• Standardkurvenquantifizierung
• Relative/Vergleichende Quantifizierung
• Normalisierung
• Referenzgenauswahl
• Analyse der Stabilität von Referenzgenen
• Alternative Normalisierungsmethoden
• Statistische Analyse und Datenvisualisierung
• Visualisierungstechniken für univariate Analysen
• Statistische Tests
• Hierarchisches Clustering
• Principal Component Analysis

PCR/qPCR Qualitative Datenanalyse

Nach Abschluss einer herkömmlichen PCR werden die Daten durch Auflösung in einem Agarosegel oder neuerdings in einem Kapillarelektrophorese-System analysiert. Bei einigen Anwendungen wird eine qPCR durchgeführt, wobei die Endpunktdaten für die Analyse verwendet werden, z. B. bei der SNP-Genotypisierung. In jedem Fall liefern die Endpunktdaten eine qualitative Analyse, nachdem die PCR die Plateauphase erreicht hat. In einigen Fällen kann es möglich sein, Endpunktdaten zu analysieren, um eine halbquantitative Analyse der PCR-Ausbeute durchzuführen, aber quantitative Messungen werden häufiger mit qPCR und der Analyse der Quantifizierungszykluswerte (C_q)¹ -Werte durchgeführt.

qPCR-Datenanalyse

In diesem Leitfaden wurden die Faktoren hervorgehoben, die zu Schwankungen bei der Messung von Nukleinsäure mittels PCR oder qPCR beitragen. Jeder dieser Faktoren sollte optimiert werden, um einen Assay zu erhalten, der der tatsächlichen Genmenge (Ziel) in der Reaktion so nahe wie möglich kommt. Das Ergebnis dieser Prozesse ist die Erstellung einer Reihe von C_q  Werten für jedes Target in jeder Probe. In diesem Kapitel wird der Prozess der Ableitung und Analyse dieser C_q -Werte vorgestellt, um zuverlässige Daten zu erhalten, die die biologische Geschichte darstellen.

Genaue C_q -Werte ableiten

Baseline-Korrektur

Ein C_q -Wert wird für jedes Target in jeder Probe bestimmt. Verschiedene Analysepakete, die mit verschiedenen Instrumenten verbunden sind, haben alternative Ansätze für die Bestimmung des C_q  (und verwenden auch alternative Bezeichnungen, z. B. C_t, C_p, Take-off-Punkt). Es würde den Rahmen dieses Leitfadens sprengen, auf die Feinheiten all dieser Algorithmen einzugehen. Allerdings sind qPCR-Messungen, die auf Amplifikationskurven beruhen, empfindlich gegenüber Hintergrundfluoreszenz. Die Hintergrundfluoreszenz kann durch eine Reihe von Faktoren verursacht werden, wie z. B. die Wahl der Plastikgefäße, verbleibende Sondenfluoreszenz, die nicht gelöscht wird, Licht, das in die Probenvertiefung eindringt, und Unterschiede in der optischen Detektion für eine bestimmte Mikrotiterplattenvertiefung. Bei gut konzipierten Assays ist der Hintergrund im Vergleich zum verstärkten Signal gering. Schwankungen im Hintergrundsignal können jedoch den quantitativen Vergleich verschiedener Proben behindern. Daher ist es wichtig, Schwankungen der Hintergrundfluoreszenz zu korrigieren, die Unterschiede in der Basislinie verursachen (Abbildung 10.1).

Abbildung 10.1 Die Komponenten der Amplifikationsdiagramme. Diese Grafik zeigt den Anstieg der Fluoreszenz mit der Anzahl der Zyklen für verschiedene Proben. Der Schwellenwert liegt oberhalb der Nachweisgrenze, aber deutlich unterhalb der Plateauphase, in der sich die Amplifikationsrate verlangsamt.

Ein gängiger Ansatz ist die Verwendung der Fluoreszenzintensität während der ersten Zyklen, z. B. zwischen den Zyklen 5 und 15, um eine konstante und lineare Komponente der Hintergrundfluoreszenz zu ermitteln. Diese wird dann als Hintergrund oder Basislinie für die Amplifikationskurve definiert. Aufgrund von transienten Effekten ist es ratsam, die ersten Zyklen (z. B. Zyklus 1 bis 5) für die Definition der Basislinie zu vermeiden, da diese häufig reaktionsstabilisierende Artefakte aufweisen. Je mehr Zyklen für die Basislinienkorrektur verwendet werden, desto besser ist die potenzielle Genauigkeit der linearen Komponente der Basislinienschwankungen. Viele Gerätesoftwarepakete ermöglichen die manuelle Einstellung der Zyklen, die für die Basisliniendefinition berücksichtigt werden sollen. Diese Funktionen sollten vom Benutzer erkundet werden, und der Versuchung, Standardeinstellungen zu akzeptieren, sollte unbedingt widerstanden werden.

Ein Beispiel für die Auswirkungen der Basislinieneinstellung ist in Abbildung 10.1 dargestellt. Wie zu sehen ist, werden die C_q -Werte und die offensichtliche Form des Amplifikationsdiagramms durch die genaue Einstellung der Basislinie beeinflusst. In diesem Beispiel wurde die Basislinie für die mit C3 bezeichnete Kurve manuell falsch eingestellt, so dass die Basislinie aus den Daten der Zyklen 5 bis 31 berechnet wurde. Dies führt dazu, dass die Kurve die Null-Basislinie (Abbildung 10.2A) mit einem C_q von 28,80 unterschreitet. Um dies zu korrigieren, werden die Rohdaten (R) betrachtet und der letzte Zyklus des linearen Hintergrunds (der letzte Zyklus vor der Amplifikation) wird identifiziert. In Abbildung 10.2B zeigt sich, dass dies der Zyklus 22 ist. Die Basislinie wird zwischen Zyklus 5 und Zyklus 22 korrekt auf Null gesetzt (Abbildung 10.2C), und die Amplifikationskurve wird anschließend korrigiert (Abbildung 10.2D). Der korrigierte C_q beträgt 26,12. Man beachte also, dass es einen erheblichen Unterschied zwischen den C_q -Werten mit den falschen und den richtigen Basislinieneinstellungen gab, was zeigt, dass die Einstellung der richtigen Basislinie eine wichtige Komponente der Datenanalyse ist.

Abbildung 10.2A-B. A) Typisches Beispiel für Daten, die unter den normalisierten Fluoreszenzwert Null fallen, wenn die Basislinie falsch eingestellt ist (blaue Amplifikationskurve). B) Rohdaten derselben Amplifikationsdiagramme, die die Grenze der linearen Basislinie zeigen und zeigen, dass die Daten nicht fehlerhaft sind.

Abbildung 10.2C-D. C) Die Grenzen für den Beginn und das Ende der Basislinie werden über die entsprechenden Softwareeinstellungen festgelegt. D) Die Anwendung der korrigierten Basislinieneinstellung führt zu einer guten Datenqualität

Einstellung des Schwellenwerts

Obwohl einige Forscher dafür plädieren, einzelne Amplifikationsplots abzubilden, um die Amplifikationseffizienz und die Zielmengen in gemessenen Proben zu schätzen^2,3,4, ist der ursprüngliche und am weitesten verbreitete Ansatz zur Ableitung von C_q die Verwendung eines Schwellenwertes. Die weite Verbreitung dieses Ansatzes ist wahrscheinlich darauf zurückzuführen, dass die Schwellenwertmethode eine einfache und effektive Quantifizierungsmethode ist.

Das Prinzip hinter der Schwellenwertmethode ist, dass, um das zugehörige Fluoreszenzsignal aus der qPCR-Amplifikation sichtbar zu machen, das Signal so ansteigen muss, dass es über der Nachweisgrenze des Geräts (und damit der Basislinie; Abbildung 10.1) liegt. Die Anzahl der dafür erforderlichen Zyklen ist proportional zur anfänglichen Kopienzahl des Targets in der Probe. Daher sind mehr Zyklen erforderlich, um das Signal über die Basislinie ansteigen zu lassen, wenn die ursprüngliche Kopienzahl niedrig ist, und weniger Zyklen, wenn die Kopienzahl hoch ist. Da die Basislinie auf die Nachweisgrenze des Systems eingestellt ist, wären Messungen an der Basislinie sehr ungenau. Anstatt bis zur Intensität der minimalen Fluoreszenz, die das System nachweisen kann, zu messen, wird daher eine höhere Fluoreszenz gewählt und ein künstlicher Schwellenwert eingeführt.

Bei der Wahl der Schwellenintensität müssen einige grundlegende Prinzipien beachtet werden. Es ist wichtig, dass der Schwellenwert für ein bestimmtes Ziel und für alle zu vergleichenden Proben auf eine feste Intensität festgelegt wird. Wenn zu viele Proben auf eine einzige Platte passen, muss ein plattenübergreifendes Kalibrierungsschema gewählt werden, z. B. die Einbeziehung einer replizierten Kontrolle, die als plattenübergreifende Kontrolle dient, oder eine serielle Verdünnung der Standardkurve. Theoretisch kann der Schwellenwert an einer beliebigen Stelle der log-linearen Phase der Amplifikationskurve festgelegt werden. In der Praxis kann die log-lineare Phase der Amplifikation jedoch durch die Drift der Hintergrundfluoreszenz-Basislinie, die Plateauphase oder Unterschiede in der Assay-Effizienz und damit im Gradienten der Amplifikationskurve bei höheren Zyklen gestört werden. Es wird empfohlen, den Schwellenwert wie folgt festzulegen:

• Ausreichend oberhalb der Hintergrundfluoreszenz-Basislinie, um zu vermeiden, dass die Amplifikationskurve den Schwellenwert aufgrund der Hintergrundfluoreszenz vorzeitig überschreitet.
• In der logarithmischen Phase der Amplifikationskurve, wo sie von der Plateauphase unbeeinflusst ist (dies ist am einfachsten zu erkennen, wenn man die Amplifikationskurven in einer logarithmischen Ansicht betrachtet, Abbildung 10.3A).
• An einer Stelle, an der die logarithmischen Phasen aller Amplifikationsdiagramme parallel sind.

Der Prozess der Schwellenwerteinstellung wird in Abbildung 10.3 gezeigt. In Abbildung 10.3A werden die Amplifikationsdiagramme auf einer logarithmischen Y-Achse betrachtet, was eine visuelle Erweiterung der logarithmischen Phase der Amplifikation ermöglicht und diese als einen linearen Teil des Amplifikationsdiagramms darstellt. Der Schwellenwert wird auf die höchste Fluoreszenzintensität (siehe Y-Achse) festgelegt, die innerhalb dieser logarithmischen Phase liegt und bei der alle Amplifikationsdiagramme parallel sind. Die Skala kehrt dann zur linearen Ansicht zurück (Abbildung 10.3B) und zeigt den höchsten Wert, der die Anforderungen an die Schwellenwerteinstellung erfüllt. Alternativ kann der Schwellenwert auch am unteren Ende dieser logarithmischen Phase eingestellt werden (Abbildungen 10.3C und 10.3D). Solange die logarithmischen Phasen der Amplifikationsdiagramme parallel sind, wird das ΔC_q zwischen den Proben durch die Schwellenwerteinstellung nicht beeinflusst.

Abbildung 10.3 Die Schwellenwerteinstellung beeinflusst den absoluten Cq-Wert und kann ΔCq zwischen den Proben beeinflussen. A). Unter Verwendung eines logarithmischen vs. linearen Plots der Daten wird der Schwellenwert auf die höchste Fluoreszenzintensität eingestellt, wobei die Amplifikationsplots parallele logarithmische Phasen zeigen. B). Die Schwellenwerteinstellung aus A) wird beibehalten und auf dem linearen vs. linearen Plot angezeigt. C). Unter Verwendung eines logarithmischen vs. linearen Plots der Daten wird der Schwellenwert auf die niedrigste Fluoreszenzintensität festgelegt, bei der die Amplifikationsplots jedoch parallele logarithmische Phasen aufweisen. D). Die Schwellenwerteinstellung aus C) wird beibehalten und auf dem linearen vs. linearen Diagramm angezeigt. In jedem Fall sind die ΔCq-Werte zwischen den Proben gleich.

Das Erfordernis einer Schwellenwerteinstellung an einer Position, an der die logarithmischen Phasen der Amplifikationsdiagramme parallel verlaufen, wird noch relevanter, wenn Daten mit höheren Zyklen in die Analyse einbezogen werden. Das Verfahren zur Einstellung der Schwellenwerte, das für die Daten in Abbildung 10.3 beschrieben wurde, wurde für einen Datensatz mit höherem C_q wiederholt und die Ergebnisse in Abbildung 10.4 dargestellt. Die resultierenden C_q -Daten in Tabelle 10.1 dienen zur Veranschaulichung der Variabilität der C_q- und, was noch wichtiger ist, der ΔC_q -Werte für drei Amplifikationsplots mit drei Schwellenwerten (Abbildung 10.4). Die ΔC_q -Werte und damit die Schätzung der relativen Menge des Targets in jeder Probe sind stark von der Einstellung des Schwellenwerts abhängig (Abbildung 10.4), da die Amplifikationsplots nicht parallel sind.

Tabelle 10.1Abhängigkeit der relativen Cq-Werte von der Position der Schwellenwerteinstellung.

Schwellenwert 1 C<q Wert	ΔCq (1)	Schwellenwert 2 Cq Wert	ΔCq (2)	Schwellenwert 3 Cq Wert	ΔCq (3)
30.67		28.77		32.33
37.38	6.71	35.17	6.4	39.31	6.98
35.03	4.36	32.99	4.22	36.88	4.55

Abbildung 10.4. Die in Abbildung 10.3 gezeigte Analyse wurde mit einem anderen Datensatz wiederholt. In diesem Fall sind die Amplifikationsdiagramme nicht parallel, was auf einen Unterschied in der Effizienz der Reaktion bei hohem Cq zurückzuführen ist. Die niedrigsten Einstellungen für A) und B) führen zu anderen ΔCq-Werten als die höchsten Einstellungen für C) und D) (Zusammenfassung in Tabelle 10.1).

qPCR-Quantifizierungsstrategien

Für eine zuverlässige Quantifizierung ist eine genaue Einstellung der Basislinie und der Schwellenwerte unabdingbar. Nach der Einstellung jedes dieser Werte wird ein C_q -Wert erzeugt, der als Grundlage für die Quantifizierung verwendet wird. Die Menge des Ziels in einer bestimmten Probe wird dann entweder mithilfe einer Standardkurve oder einer relativen/vergleichenden Quantifizierung bestimmt.

Standardkurvenquantifizierung

Wie der Name schon sagt, erfordert die Standardkurvenquantifizierung die Verwendung einer Standardkurve zur Bestimmung der Zielmengen in Testproben. Alle für Proben ermittelten Mengen sind daher relativ zu der der Standardkurve zugeordneten Menge. Dies erfordert die Verwendung zusätzlicher, externer Standards neben jedem Satz von Probenreaktionen. Die Auswahl des Materials für die Standardkurve ist wichtig, um potenzielle Quantifizierungsunterschiede aufgrund von Unterschieden zwischen den Assay-Effizienzen in den Proben und in den Standards zu eliminieren. Die Primer-Bindungsstellen der externen Standards müssen mit denen des Targets übereinstimmen, die gleichen Sequenzen wie das Target enthalten, eine ähnliche Komplexität aufweisen und so ähnlich wie möglich gehandhabt werden. Daher ist es bei der Messung der Konzentration eines Targets in cDNA vorzuziehen, die gleiche cDNA in einer seriellen Verdünnung einer Kontrollprobe zu messen. Bei einigen Studien gibt es jedoch praktische Gründe, die dies verhindern, so dass es wichtig ist, die Probenbedingungen so genau wie möglich zu reproduzieren, z. B. durch Zugabe von gDNA von einer Spezies, die nicht mit der zu testenden Spezies verwandt ist, zu einem künstlichen Oligonukleotidstandard oder einem linearisierten Plasmid, das die Standardsequenz trägt. Sobald ein geeignetes Konstrukt oder Amplikon identifiziert ist, wird eine Standardkurve aus seriellen Verdünnungen erstellt. Der C_q für das Ziel wird für jeden der Standards bestimmt und gegen die Konzentration oder den relativen Konzentrations-/Verdünnungsfaktor auf einer logarithmischen Skala aufgetragen. Daraus ergibt sich eine Standardkurve, die dann zur Bestimmung der Konzentrationen der Testproben durch Vergleich der C_q -Werte aus der Amplifikation der unbekannten Proben verwendet wird. Bei Verwendung einer Standardkurve zur Quantifizierung muss der Schwellenwert für die Bestimmung von C_q für den Standard und für die Proben auf derselben Platte konstant gehalten werden. Der Schwellenwert kann von Platte zu Platte unterschiedlich sein.

Relative/vergleichende Quantifizierung

Bei der relativen oder vergleichenden Quantifizierung wird der Unterschied in C_q als Bestimmungsfaktor für die Unterschiede in der Konzentration der Zielsequenz in verschiedenen Proben verwendet. Anstatt die Menge des Ziels pro Probe zu messen, wie es bei der Standardkurvenmethode der Fall ist, führt dies zu Datensätzen, die fache Veränderungen zwischen den Proben zeigen.

In der ursprünglichen Form dieses Ansatzes⁵ wurde die Effizienz aller Assays mit 100% angenommen, was zu der Annahme führte, dass ein C_q Unterschied von 1 (ΔC_q = 1) das Ergebnis eines 2-fachen Unterschieds im Target war. Zur Bestimmung einer Fold-Change im Target oder Gene of Interest (GOI) müssen die Daten auch auf eine Ladekontrolle bezogen werden (Referenzgen, ref; siehe nachfolgende Ausführungen zur Datennormalisierung).

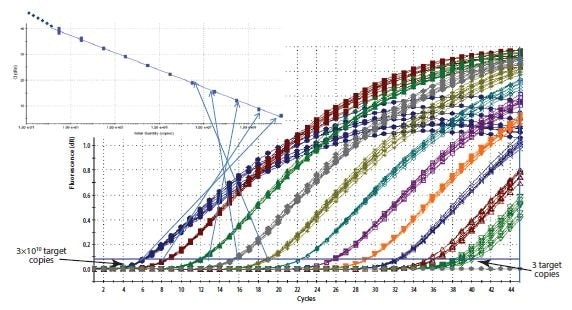
Abbildung 10.5. Erstellung einer Standardkurve. Der für jede Probe einer Verdünnungsreihe erfasste Cq-Wert wird auf einer logarithmischen Skala gegen die relative Konzentration aufgetragen.

In Gleichung 1 wird das Verhältnis der GOI, nach Korrektur auf das ref-Gen, in 2 Proben (A relativ zu B) wie folgt gemessen: 2 (unter der Annahme von 100 % effizienten Reaktionen) hochgerechnet auf die Potenz der Unterschiede in den C_q -Werten für die GOI geteilt durch 2 hochgerechnet auf die Potenz der Unterschiede in den C_q -Werten für das Referenzgen

Gleichung 1. Original (Livak) Relatives Quantifizierungsmodell.

Wie jedoch in Assay-Optimierung und Validierung dargestellt, variieren die Effizienzen der Reaktionen beträchtlich, was einen großen Einfluss auf die Daten haben kann. Daher wurden die Annahmen in Gleichung 1 angesprochen (Gleichung 2)⁶, so dass die Unterschiede in den Reaktionswirkungsgraden in die Analysen einbezogen werden konnten. In diesem Fall wird der Amplifikationsfaktor 2 durch die tatsächliche Effizienz der PCR ersetzt (wie durch eine Standardkurvenanalyse bestimmt; siehe Assay-Optimierung und Validierung).

Gleichung 2. Effizienz Angepasstes (Pfaffl) Relatives Quantifizierungsmodell

Als Beispiel für die Anwendung des an die Effizienz angepassten (Gleichung 2) relativen Quantifizierungsmodells wird in Tabelle 10.2 eine Reihe von C_q -Werten dargestellt. Die Effizienz für die GOI beträgt 1,8 und für das ref-Gen 1,94.

Tabelle 10.2Arbeitsbeispiel zur Berechnung der Fold Change (Ratio) unter Verwendung von Cq-Differenzen.

Schwellenwert 1	Cq GOI	ΔCq GOI	EΔCq GOI	Cq Ref	ΔCq Ref	EΔCq Ref	EΔCq GOI EΔCq Ref
1	34			18				/td>
2	26	8	110.2	17	1	1.94	56.8

Dies ist ein sehr einfaches Beispiel für eine Studie mit der Anforderung, die Fold-Differenz zwischen einem Gen in zwei Proben und nach Normalisierung auf ein einzelnes Referenzgen zu messen. Das Verhältnis zeigt die fache Veränderung der GOI in Probe 2 im Vergleich zu Probe 1, nach Korrektur auf das einzelne Referenzgen. Es hat sich jedoch gezeigt, dass die Auswahl eines einzigen, geeigneten Referenzgens oft unmöglich ist, und daher wurden anspruchsvollere Ansätze für die Normalisierung vorgeschlagen.

Normalization

Das Hauptziel der meisten PCR-basierten Experimente besteht darin, die grundlegende Frage zu klären, ob das Ziel in der Probe vorhanden ist (unbekannt, UNK). Am einfachsten lässt sich diese Frage beantworten, indem man ein Gel herstellt und die Fragmente auf das Vorhandensein oder Fehlen des gewünschten GOI untersucht. Wenn das Fragment vorhanden ist, gibt die Bestätigung der Fragmentgröße die Gewissheit eines positiven Ergebnisses. Ist es jedoch nicht vorhanden, besteht die Möglichkeit eines falsch negativen Ergebnisses. Daher ist es wichtig, den Test zu wiederholen und mindestens eine weitere PCR durchzuführen, die als Lade- und Positivkontrolle dient. Der universelle Inhibitionskontrolltest SPUD (siehe Probenaufreinigung und Qualitätsbewertung) kann verwendet werden, um das Vertrauen in ein negatives Ergebnis zu stärken. Ein alternativer Ansatz ist die Durchführung eines Assays, der für ein oder mehrere Referenzgene spezifisch ist. Traditionell wurden PCR-Assays zum Nachweis der Referenzgene GAPDH, 18S ribosomale RNA oder β-Actin zusammen mit denen für die GOI durchgeführt und die resultierenden Fragmente auf einem Gel sichtbar gemacht. GAPDH, 18S ribosomale RNA und β-Actin werden konstitutiv exprimiert und wurden daher als Ladekontrollen in semi-quantitativen Analysen verwendet. Es stellte sich jedoch bald heraus, dass diese Gene nicht ubiquitär in allen Zellen in der gleichen Konzentration exprimiert werden, unabhängig vom Versuchsaufbau. Daher entstand der Bedarf an einer stabilen Referenz, wenn das Ziel darin bestand, relative Nukleinsäurekonzentrationen zu messen, in der Regel cDNA, aber auch gDNA, wenn z. B. die Kopienzahlvariation eines Gens untersucht werden sollte.

Normalisierung ist der Prozess der Korrektur technischer Messungen auf eine stabile Referenz, um echte biologische Variation zu untersuchen. Es gibt viele Methoden zur Normalisierung technischer Unterschiede, was bedeutet, dass der geeignete Ansatz für das spezifische Experiment ausgewählt und validiert werden muss⁷. Es ist von entscheidender Bedeutung zu erkennen, dass die Anwendung ungeeigneter Normalisierungstechniken für den gesamten Analyseprozess nachteiliger sein kann, als überhaupt nicht zu normalisieren⁸.

Die Auswirkung der Probenqualität auf die Assay-Normalisierung

Die Auswirkung der Probenintegrität und -reinheit auf die Zielmengenmessungen mittels qPCR und RT-qPCR wurde ausführlich diskutiert (Probenaufreinigung und Qualitätsbewertung, Probenqualitätskontrolle und Reverse Transkription, Reverse Transkription). Es wurde nachgewiesen, dass Inhibitoren in der Probe und der RNA-Abbau einen unterschiedlichen Einfluss auf die Messung eines bestimmten Ziels⁹ haben. Inhibitoren wirken sich auf die Messung jedes Targets aus, jedoch in unterschiedlichem Maße, je nach Testdesign. Der Abbau der Gesamt-RNA wirkt sich auf die Messung von mRNA und miRNA¹⁰ aus, was wiederum in hohem Maße von der gesamten Versuchsplanung abhängt. Daher ist es wichtig, die Auswirkungen der Template-Konzentration auf die RT-Reaktion und die Auswirkungen der Probenqualität auf die Daten nach der Normalisierung zu berücksichtigen. Die Normalisierung kann die Auswirkungen von Assays oder Proben geringer Qualität nicht ausgleichen (siehe Assay-Optimierung und Validierung).

Normalisierungsansätze

Generell wirken Normalisierungsmethoden der Variabilität entgegen, die während des mehrstufigen Prozesses, der zur Durchführung einer qPCR-Analyse erforderlich ist, eingeführt werden kann (Abbildung 10.6). Die Anwendung der Normalisierung in einer beliebigen Phase des Prozesses kann jedoch technische Fehler und/oder Verzerrungen, die in einer früheren oder späteren Phase eingeführt wurden oder werden, nicht ausgleichen. Normalisierungsmethoden schließen sich nicht gegenseitig aus, so dass eine Kombination von Kontrollen empfohlen wird¹¹.

Abbildung 10.6. Die qPCR ist ein mehrstufiger Prozess und jeder Schritt muss kontrolliert werden. Die Normalisierung muss im Rahmen einer Reihe von Kontrollen berücksichtigt werden.

Das Ziel der Normalisierung besteht darin, einen stabilen Bezugspunkt zu schaffen, auf den die Messungen bezogen werden können; daher muss die Wahl des Normalisierungsfaktors eine Messung sein, die während des gesamten Experiments stabil ist. Dies kann ein stabiles Referenzgen oder eine der Alternativen sein, wie Zellzahl, Gewebemasse, RNA/DNA-Konzentration, ein externer Spike¹² oder ein repräsentatives Maß für die global exprimierten Gene.

Referenzgenauswahl

Referenzgene sind Ziele, deren Menge sich durch das Experiment nicht ändert. Bei der Quantifizierung von DNA-Kopienzahlvariationen, bei denen sich die Anzahl der Kopien der interessierenden Sequenz ändern kann, wird die Messung einfach normalisiert, indem eine alternative genomische Region ausgewählt wird, von der bekannt ist, dass sie sich nicht ändert. Ein Beispiel für die Anwendung dieses Verfahrens ist die Messung der genomischen Amplifikation des humanen epidermalen Wachstumsfaktor-Rezeptors 2 (HER-2)¹³. Die genomische HER-2-Instabilität ist ein prognostischer Indikator bei Brustkrebs, und die genaue Messung des HER-2-Amplifikationsstatus ist für die Behandlung der Patientinnen wichtig. Der HER-2-Status kann mittels qPCR gemessen werden, indem die HER-2-Kopien mit einem anderen genomischen Ziel verglichen werden, das als Kontrolle dient.

Bei der Messung der Genexpression sind Referenzgene Ziele mit mRNA-Konzentrationen, die sich durch das Experiment nicht verändern. Ein Beispiel wäre eine Studie, in der die Auswirkung auf die Expression von Gen X nach Zugabe einer mitogenen Verbindung zu einer Zellmonolage gemessen wird. Um die Veränderung des Gens X zu messen, wird ein Referenzpunkt benötigt. Daher wird ein anderes Gen (oder mehrere Gene), von dem/denen bekannt ist, dass es/sie nicht durch das betreffende Mitogen beeinflusst wird/werden, ebenfalls gemessen. Dies stellt den Forscher vor die unmittelbare Herausforderung, ein mRNA-Ziel zu finden, das durch das experimentelle Verfahren nicht beeinflusst wird, bevor er die GOI untersuchen kann. Dieser Prozess der Validierung von Referenzgenen ist grundlegend für eine genaue Messung der GOI. Der am weitesten verbreitete Ansatz zur Normalisierung besteht darin, diesen Prozess zu ignorieren und die Genexpressionsdaten auf ein einziges, nicht validiertes Referenzgen zu normalisieren. Diese Praxis wird nicht empfohlen und steht im direkten Widerspruch zu den MIQE-Richtlinien¹. Die Quantifizierung von mRNA durch RT-qPCR wurde routinemäßig durch die falsche Wahl von Referenzgenen beeinträchtigt. Es ist nicht akzeptabel, die relativ weit verbreitete Praxis zu befolgen, ein Referenzgen zu verwenden, weil die Primer bereits im Gefrierschrank liegen, weil es in der Vergangenheit für Northern Blots verwendet wurde, weil es von einem Kollegen verwendet wird oder weil es in einem anderen Labor für ein anderes Experiment verwendet wurde. Referenzgene müssen unter bestimmten experimentellen Bedingungen validiert werden, um sicherzustellen, dass das betreffende Referenzgen nicht durch das Experiment beeinträchtigt wird. Wenn diese Validierung nicht durchgeführt wird und das Referenzgen durch das Experiment beeinflusst wird, könnten die Ergebnisse falsch sein, und die anschließenden Interpretationen führen wahrscheinlich zu bedeutungslosen Daten⁸.

Es gibt eine Reihe von wissenschaftlicher Literatur, in der verschiedene Methoden zur Normalisierung^7-14 beschrieben werden, sowie eine Fülle von Veröffentlichungen, in denen die Protokolle beschrieben werden, die erforderlich sind, um die am besten geeigneten Normalisierungsgene für ein bestimmtes experimentelles Szenario zu ermitteln. Während in der Vergangenheit die Frage im Vordergrund stand, ob ein einzelnes oder mehrere Referenzgene ausgewählt werden sollten, haben sich die aktuellen Best Practices aufgrund der niedrigeren Betriebskosten auf die Messung mehrerer Referenzgene verlagert.

Die Auswahl stabiler Referenzgene erfordert, dass der Analytiker die Stabilität der qPCR für eine Reihe (in der Regel 10 bis 20 Gene) von mRNA-Zielkandidaten⁷ an einer Teilmenge von Proben bewertet, die die Test- und Kontroll-mRNAs repräsentieren. Ein vollständiges Protokoll finden Sie in Anhang A, Protokolle, dieses Leitfadens und kann in Kombination mit verschiedenen Analysemethoden unter Verwendung von Programmen wie REST¹⁵, GeNorm¹⁴, Bestkeeper¹⁶ oder NormFinder¹⁷ verwendet werden. Dieses Verfahren wird im folgenden Abschnitt "Analyse der Stabilität von Referenzgenen" näher beschrieben.

Analyse der Stabilität von Referenzgenen

Das Referenzgen ist buchstäblich der Dreh- und Angelpunkt für qPCR-Assays zur relativen Quantifizierung. Daher ist es für die Zuverlässigkeit des gesamten Assays entscheidend, dass das Referenzgen stabil ist. Wenn die Expression des Referenzgens zwischen den Proben schwankt, wird diese Schwankung direkt auf die Quantifizierungsergebnisse übertragen, und die zusätzliche Schwankung kann den gewünschten beobachtbaren biologischen Effekt verschleiern oder, was noch schlimmer ist, einen völlig künstlichen Anschein eines biologischen Effekts erwecken, der nichts mit dem eigentlichen Gen von Interesse zu tun hat. Aus diesen Gründen wird dringend empfohlen, mehrere Sicherheitsmaßnahmen zu ergreifen, um die Variabilität der Referenzgene unbedeutend zu machen und die Messungen der biologischen Wirkungen so aussagekräftig wie möglich zu gestalten.

Die wohl wichtigste Sicherheitsmaßnahme besteht darin, nicht nur ein, sondern zwei oder mehr Referenzgene zu verwenden. Die Expression mehrerer Referenzgene kann gemittelt werden, um die technische Variabilität aufgrund der Normalisierung zu verringern. Dies kann nützlich sein, um die Signifikanz bei Messungen kleiner biologischer Effekte zu verbessern. Noch wichtiger ist jedoch, dass zwei oder mehr Referenzgene gegenseitige Kontrollen für die Aufrechterhaltung der Stabilität und die Kontrolle unerwarteter Ereignisse bieten, die das Expressionsniveau eines der Referenzgene beeinflussen könnten. Bei einem einzigen Referenzgen besteht die Gefahr, dass unerwartete Einflüsse auf die Genexpression im Assay unentdeckt bleiben.

Eine weitere Sicherheitsmaßnahme ist die Verwendung von mehr als einer Methode zur Identifizierung stabiler Referenzgene. Das folgende Beispiel veranschaulicht mehrere Aspekte der Normalisierung von Referenzgenen, einschließlich eines möglichen Vorteils der Verwendung von geNorm- und NormFinder-Methoden für denselben Datensatz.

Tabelle 10.3 enthält eine Liste von Referenzgen-Kandidaten, die während eines Workshops, den wir zuvor mit dem EMBL durchgeführt haben, bewertet wurden. Die Proben wurden aus einer menschlichen Zellkultur in zwei verschiedenen Behandlungsgruppen gewonnen. Dieser Datensatz wird verwendet, um Aspekte der Validierung von Referenzgenen zu demonstrieren.

Beide Algorithmen, NormFinder und geNorm, wurden unter der Annahme entwickelt, dass das Testen einer Vielzahl von Referenzgenkandidaten dazu verwendet werden kann, die Stabilität einzelner Referenzgenkandidaten zu bewerten. Diese Annahme kann zutreffen, wenn zum Beispiel alle Referenzgenkandidaten stochastisch um stabile Expressionsniveaus herum variieren. In der Realität ist dies jedoch nicht unbedingt der Fall. Um irreführende Ergebnisse zu vermeiden, ist es daher ratsam, regulierte und insbesondere ko-regulierte Referenzgenkandidaten zu vermeiden.

Tabelle 10.3Beispiel für ein Referenzgen-Panel zur Validierung von Referenzgenen. Für eine genaue Leistung ist es wichtig, ko-regulierte Referenzgen-Kandidaten zu vermeiden.

	Referenzgen	Akzessionsnummer.
1	18S	NR_03286
2	ACTB	NM_001101
3	ATP5B	NM_001686
4	B2M	NM_004048
5	CANX	NM_001024649
6	EIF4A2	NM_001967
7	CAPDHa	NM_002046
8	GAPDHb	NM_002046
9	GUSB	NM_000181
10	PPIA	NM_021130
11	SDHA	NM_004168
12	TBP	NM_003194
13	TUBB	NM_178012
14	UBC	NM_021009
15	YWHAZ	NM_003406

Die Liste der Referenzgen-Kandidaten in Tabelle 10.3 wurde so ausgewählt, dass Gene ausgewählt wurden, die verschiedenen Funktionsklassen angehören, wodurch die Wahrscheinlichkeit einer gemeinsamen Regulierung der Gene verringert wird. Eine bemerkenswerte Ausnahme ist GAPDH, das hier in zwei Versionen vorhanden ist. Obwohl dies keinen Einfluss auf diese Analyse hat, ist es die beste Praxis, Mehrfacheinträge von Genen zu vermeiden, bei denen der Verdacht besteht, dass sie koreguliert sind.

Der erste Algorithmus, der vorgestellt wird, ist geNorm. Dieser liefert eine Bewertung der Genstabilität durch die Berechnung eines Genstabilitätsmaßes, des sogenannten M-Wertes, der auf paarweisen Vergleichen zwischen dem analysierten Referenzgenkandidaten und allen anderen Referenzgenkandidaten im Datensatz basiert. Es wird iterativ durchgeführt, d. h. in diesem Beispiel wird das Verfahren zunächst für alle 15 Referenzgenkandidaten durchgeführt, das am wenigsten stabile wird entfernt, der Prozess wird für die verbleibenden 14 Kandidaten wiederholt, der zweite am wenigsten stabile Kandidat wird entfernt, und so weiter, bis zwei Referenzgene übrig bleiben.

Es kann Zeiten geben, in denen die Identifizierung des stabilsten Referenzgens besonders schwierig ist. Dies kann der Fall sein, wenn alle Referenzgen-Kandidaten schlecht abschneiden. Ein anderer Fall kann sein, dass alle Referenzgen-Kandidaten gut abschneiden. Um zwischen diesen beiden Fällen zu unterscheiden, ist eine nützliche Richtlinie, dass Referenzgene mit einem M-Wert unter 0,5 als stabil exprimiert angesehen werden können.

Der zweite Algorithmus, der demonstriert werden soll, ist NormFinder, ein frei verfügbares Paket zur Analyse von Referenzgenen (Anhang B, Zusätzliche Ressourcen). Der zugrunde liegende Algorithmus verfolgt bei der Bewertung der Stabilität von Referenzgenen einen ANOVA-ähnlichen Ansatz, bei dem die Gesamt- und Untergruppen auf Abweichungen untersucht werden. Ein Vorteil ist, dass die erhaltenen Maße direkt mit den Genexpressionsniveaus verbunden sind. Eine Standardabweichung von 0,20 in C_q -Einheiten entspricht daher einer Variation von etwa 15 % in den Kopienzahl-Expressionsniveaus des jeweiligen Referenzgenkandidaten.

Zur Vereinfachung wird in dieser Demonstration auf beide Analysepakete mit der Datenanalysesoftware GenEx (MultiD) zugegriffen, sie sind jedoch auch als unabhängige Pakete erhältlich (Anhang B, Zusätzliche Ressourcen).

Die Balkendiagramme in Abbildung 10.7 veranschaulichen Referenzgene, die nach ihren jeweiligen Stabilitätsmaßen unter Verwendung beider Algorithmen geordnet sind. Zusätzlich zeigt ein Diagramm, das die kumulierte Standardabweichung von NormFinder zeigt, dass eine Kombination von bis zu den drei besten Referenzgenen Stabilitätsverbesserungen bringen kann.

Abbildung 10.7. Balkendiagramme mit Stabilitätsmaßen: M-Werte für geNorm und Standardabweichungen für NormFinder. Darüber hinaus zeigt ein Diagramm mit der kumulierten Standardabweichung von NormFinder, dass eine Kombination von bis zu den drei besten Referenzgenen zu Stabilitätsverbesserungen führen kann. Der Datensatz wurde aus Assays generiert, die für die in Tabelle 10.3 aufgeführten Referenzgenkandidaten entwickelt und an einer menschlichen Zellkultur in zwei verschiedenen Behandlungsgruppen gemessen wurden. Man beachte, dass in diesem Fall die Algorithmen für die Stabilität der Referenzgene, geNorm und NormFinder, sich nicht über die besten Referenzgene einig sind.

Abbildung 10.8. Mittleres zentriertes Expressionsprofil der Referenzgenkandidaten der beiden Proben in jeder Behandlungsgruppe. Die Proben 1 und 2 gehören zur ersten Behandlungsgruppe und die Proben 3 und 4 gehören zur zweiten Behandlungsgruppe. Die Expressionsprofile von SDHA und CANX sind in rot dargestellt. Das Expressionsprofil von UBC ist in gelb dargestellt. In der Tabelle sind die gemessenen Cq-Werte des Datensatzes aufgeführt.

Aufgrund der abweichenden Expressionsprofile ist es möglich, dass SDHA und CANX durch die verschiedenen Behandlungsalternativen reguliert werden und daher nicht als Referenzgene geeignet sind. Werden diese aus dem Datensatz entfernt und die Analyse wiederholt, stimmen beide Algorithmen überein und die beste Wahl der Referenzgene sind EIF4A2 und ATP53 (Abbildung 10.9). Auch bei der NormFinder-Berechnung der kumulierten Standardabweichungen zeigt sich, dass die Hinzunahme weiterer Referenzgene die Stabilität nicht verbessert.

Abbildung 10.9. Die Prüfung der Expressionsprofile und der gemessenen Cq-Werte (Abbildung 10.8) gab Anlass zu der Sorge, dass SDHA und CANX in dem angewandten Assay möglicherweise koreguliert werden. Diese Koregulation könnte die Algorithmen für die Stabilität der Referenzgene stören. Balkendiagramme mit Stabilitätsmaßen: A) M-Werte für geNorm und B) Standardabweichungen für NormFinder. Der Datensatz ist derselbe wie in Abbildung 10.8, mit der Ausnahme, dass die Daten für SDHA und CANX entfernt wurden. Beachten Sie, dass die Algorithmen für die Stabilität der Referenzgene geNorm und NormFinder bei diesem reduzierten Datensatz hinsichtlich der besten Referenzgene übereinstimmen.

Die Analyse der Daten in diesem Beispiel dient zur Veranschaulichung, dass die parallele Verwendung von geNorm und NormFinder die Identifizierung koregulierter Referenzgene ermöglicht und dass das Entfernen dieser Gene aus weiteren Studien eine endgültige Identifizierung von Referenzgenen ergibt, die mit größerer Sicherheit angenommen werden können als nach der Verwendung einer einzelnen Analyse. Die Identifizierung und Auswahl von stabilen Referenzgenen führt zu einer größeren Sicherheit der Datenanalyse.

Alternative Normalisierungsmethoden

Obwohl die Normalisierung auf Referenzgene die gängigste Methode zur Assay-Normalisierung ist, gibt es Situationen, in denen dieser Ansatz nicht geeignet ist, z. B. wenn eine große Anzahl von Genen in einer heterogenen Gruppe von Proben verglichen werden soll oder wenn miRNA-Profile erstellt werden. In diesen Fällen muss eine alternative Strategie gewählt werden.

Normalisierung auf die Gewebemasse oder Zellzahl

Die Messung der Zellzahl oder der Gewebemasse als Normalisierungsfaktor ist nicht so einfach, wie es zunächst scheint. Zellkulturexperimente lassen sich relativ leicht anhand der Zellzahl normalisieren. Die Zugabe einer Behandlung kann sich jedoch auf die Zellmorphologie auswirken, was das Verhältnis von Zellzahl zu insgesamt exprimierter RNA/Genen im Vergleich zu einer Kontrollkultur erschwert. Die experimentelle Behandlung kann zur Produktion zusätzlicher zellulärer Matrix führen, was Unterschiede in der Effizienz der Nukleinsäureextraktion zur Folge hat.

Biologisches Gewebe kann sowohl innerhalb eines Probanden als auch zwischen verschiedenen Probanden sehr heterogen sein, wobei die Unterschiede noch größer sind, wenn gesundes Gewebe mit krankem Gewebe verglichen wird. Selbst scheinbar weniger komplexe Gewebe wie Blut können sich in der Zellzahl und -zusammensetzung erheblich unterscheiden, so dass die Genexpression zwischen scheinbar gesunden Spendern beträchtlich variiert¹⁸.

Jede Verzögerung bei den Verfahren zur Reinigung der Nukleinsäure führt zu Veränderungen in der gemessenen RNA. Beispielsweise führen Verzögerungen bei der Aufbereitung von peripheren mononukleären Blutzellen und der Extraktion von RNA aus den Zellen zu erheblichen Veränderungen der Genexpression¹⁹. Die Methoden, die den Extraktionsverfahren zugrunde liegen, sind ebenfalls eine wichtige Quelle für technische Abweichungen. Selbst das für die Entnahme von aus Blut gewonnenen Zellen gewählte Isolierungsverfahren und die RNA-Aufreinigung führen zu Unterschieden in den offensichtlichen Genexpressionsprofilen²⁰. Daher muss bei der Normalisierung zunächst sichergestellt werden, dass die Entnahme und Verarbeitung aller Proben absolut identisch ist. Anschließend muss eine ausreichende Qualitätskontrolle durchgeführt werden, um die Konzentration, Integrität und Reinheit der Proben sicherzustellen (Probenaufreinigung und Qualitätsbewertung und zugehörige Protokolle in Anhang A).

Normalisierung auf RNA-Konzentration

Als Minimum ist eine Abschätzung der Template-Konzentration (DNA für qPCR oder RNA für RT-qPCR) wichtig und, wie in Probenaufreinigung und Qualitätsbewertung ist es entscheidend, dass für alle Messungen dasselbe Gerät verwendet wird, da die Bestimmung der Nukleinsäurekonzentration ebenfalls variabel und technikabhängig ist.

Bei der Messung der Gesamt-RNA-Konzentration besteht der überwiegende Teil der Probe aus rRNA und nur ein kleiner Teil aus der mRNA, die bei der Untersuchung der Genexpression von Interesse ist, bzw. der sncRNA bei der Untersuchung der Genexpressionsregulation. Das bedeutet, dass die Gesamt-RNA-Konzentration ansteigt, wenn die rRNA-Konzentration geringfügig ansteigt, die mRNA-Konzentration jedoch konstant bleibt. Die mRNA-Konzentration muss erheblich ansteigen, um einen offensichtlichen Anstieg der Gesamt-RNA-Konzentration zu bewirken. Daher ist die rRNA-Konzentration ein unzuverlässiges Maß für die mRNA-Konzentration, aber für viele Protokolle ist eine gleiche RNA-Konzentration erforderlich, um eine genaue reverse Transkription zu gewährleisten (siehe Umgekehrte Transkription).

Normalisierung auf die globale Genexpression

Bei der Messung einer großen Anzahl von Targets kann der Analytiker den globalen Mittelwert der gesamten Genexpression schätzen und regulierte RNA-Sequenzen identifizieren, die von diesem Mittelwert abweichen. Dieser Ansatz wird üblicherweise zur Normalisierung von Genexpressions-Arrays verwendet. Es ist eine wertvolle Alternative zur Verwendung von Referenzgenen und kann vorzuziehen sein, wenn viele Targets gemessen werden.

Ein weiterer kürzlich erforschter Ansatz ist die Messung endogen exprimierter Wiederholungselemente (ERE), die in vielen mRNAs vorhanden sind. Viele Arten enthalten diese Wiederholungselemente (ALU bei Primaten, B-Elemente bei Mäusen), die eine Schätzung des mRNA-Anteils ermöglichen. Die Messung dieser Zielsequenzen hat sich als herkömmliches Normalisierungssystem erwiesen⁹ (Le Bert, et al., in Vorbereitung) und kann eine universelle Lösung oder eine Alternative für komplexe Experimente bieten, bei denen stabile Referenzgenkombinationen nicht verfügbar sind.

Normalisierung von miRNA-Daten

Bislang gibt es keine Berichte über ein universelles miRNA-Referenzgen. Daher ist die Auswahl des Normalisierungssystems noch eher empirisch. Wenn möglich, können stabile invariante miRNAs aus genomweiten Ansätzen, d.h. Microarrays, identifiziert werden. Kleine nukleolare RNAs (snoRNAs) wurden ebenfalls als Referenzgene verwendet. Die globale Genexpression ist ebenfalls eine nützliche Methode zur Normalisierung der miRNA-Expression, wenn eine stabile Referenz unbekannt ist und mehrere hundert Targets analysiert wurden^21,22,23. Diese Methode ist eher für diejenigen geeignet, die Ansätze verwenden, bei denen alle miRNAs als cDNA in einer multiplexen Form erfasst werden, z. B., Exiqon und miQPCR-Systeme (siehe Castoldi et al. in PCR Technologies, Current Innovations²⁴).

Biologische und technische Replikate

Der Zweck der Normalisierung besteht darin, systematische Fehler zu vermeiden und die Datenvariabilität für die spätere statistische Analyse zu verringern. Ein weiterer wichtiger Aspekt der Datenaufbereitung für die statistische Analyse ist die Verwendung von Datenwiederholungen.

Biologische Wiederholungen sind für die statistische Analyse unbedingt erforderlich. Statistische Signifikanzniveaus werden oft mit einem Signifikanz-Cut-off von 5 % festgelegt. Bei biologischen Effekten, die in der Nähe eines solchen Signifikanzniveaus liegen, kann es erforderlich sein, mindestens 20 biologische Wiederholungen zu haben, um das Signifikanzniveau des Tests zu bestimmen (1:20 entspricht 5 %). Es wurde sogar vorgeschlagen, dass für eine genaue Schätzung der Signifikanz²⁵ mindestens die 50-fache Anzahl von Beobachtungen aufgezeichnet werden muss, d.h. in der Größenordnung von tausend biologischen Proben. Natürlich sind biologische Wiederholungen in dieser Größenordnung aus praktischen Gründen nur selten möglich. Außerdem hängen genaue Schätzungen der Anzahl der erforderlichen biologischen Wiederholungen zur Erreichung eines bestimmten Signifikanzniveaus auch vom Grad der Variabilität der Daten ab. Dennoch ist es wichtig zu erkennen, dass ein häufiger Fehler darin besteht, die Anzahl der erforderlichen biologischen Wiederholungen zu unterschätzen, um zu zuverlässigen Schlussfolgerungen zu gelangen. Es wird empfohlen, eine erste Pilotstudie durchzuführen, um die inhärente Variabilität des Assays und die potenzielle Größe des beobachtbaren biologischen Effekts zu bewerten, um eine gute Grundlage für die Schätzung der erforderlichen Anzahl biologischer Replikate zu haben²⁶.

Technische Replikate werden nicht direkt für die statistische Analyse verwendet. Stattdessen werden technische Replikate zur Sicherung von Proben (für den Fall, dass einige Proben bei der technischen Bearbeitung verloren gehen) und zur besseren Bewertung der Datengenauigkeit verwendet. Technische Replikate können die Datengenauigkeit verbessern, wenn die Annahme zutrifft, dass sie in jeder Phase des technischen Bearbeitungsprozesses stochastisch um den genauen Messwert schwanken. Der Durchschnitt der technischen Replikate liegt näher an der genauen Messung. Die Auswirkung der Mittelwertbildung bei technischen Wiederholungen lässt sich anhand der Größe des Konfidenzintervalls in einem simulierten Datensatz mit einer vorgegebenen Variabilität, d. h. einer Standardabweichung von 1, veranschaulichen. Wie in Tabelle 10.4 zu sehen ist, wird das Konfidenzintervall mit zunehmender Zahl der technischen Wiederholungen (Proben) kleiner, was auf eine genauere Schätzung der genauen Messung hinweist. Außerdem ist die Verkleinerung des Konfidenzintervalls bei einer geringen Anzahl von technischen Wiederholungen am dramatischsten. Eine Erhöhung der Anzahl der Wiederholungen von 2 bis 3 verringert das Konfidenzintervall von 8,99 auf 2,48, d. h. eine mehr als dreifache Verbesserung der Präzision bei der Schätzung der genauen Messung. Zusätzliche Wiederholungen verbessern zwar weiterhin die Schätzung der Messgenauigkeit, aber der Effekt ist abnehmend. Daher ist es offensichtlich, dass es in Fällen, in denen die Variabilität der technischen Handhabung ein Problem darstellt, von großem Vorteil sein kann, Dreifach- statt Doppelversuche zu verwenden.

Tabelle 10.4Größe der Konfidenzintervalle der geschätzten Mittelwerte, normalisiert auf eine Standardabweichung von 1 und ein α-Konfidenzniveau von 5 %. Das Konfidenzintervall wird mit zunehmender Anzahl technischer Wiederholungsproben kleiner, was auf eine präzisere Schätzung der genauen Messung bei einer höheren Anzahl von Wiederholungsproben hinweist.

Konfidenzintervalle der geschätzten Mittelwerte
Stichproben	Cl (α=0.05 und SD=1)
2	8.99
3	2.48
4	1.59
5	1.24
10	0.72
20	0.47
50	0,28

Technische Replikate können in mehreren Phasen des Probenhandhabungsprozesses gesammelt werden, einschließlich RNA-Extraktion, reverser Transkription und qPCR-Detektion. Werden technische Replikate in mehreren Phasen festgestellt, wird ein verschachtelter Versuchsplan erstellt. Eine Pilotstudie, die sich einen verschachtelten Versuchsplan zunutze macht, kann dazu beitragen, die Phasen der Probenhandhabung zu ermitteln, die am meisten zu technischen Handhabungsfehlern beitragen, und auf der Grundlage dieser Informationen kann ein optimaler Probenahmeplan berechnet werden²⁷.

Statistische Analyse und Datenvisualisierung

Die wissenschaftliche Analyse biologischer Daten konzentriert sich auf die Formulierung und Prüfung von Hypothesen. Die Formulierung einer Hypothese erfordert ein detailliertes Verständnis der Bedingungen und Variablen des Versuchs. Die erfolgreiche Prüfung einer Hypothese erfordert eine sorgfältige Durchführung und einen geeigneten Versuchsplan, um das gewünschte beobachtbare Signal zu maximieren und gleichzeitig die technische Variabilität zu minimieren. In diesem Zusammenhang ist es sinnvoll, zwischen explorativen und bestätigenden Studien zu unterscheiden (Abbildung 10.10).

Abbildung 10.10. Flussdiagramm zur Veranschaulichung der Vorgänge bei explorativen und konfirmatorischen statistischen Analysen. Die linke Seite der Abbildung, vor dem gestrichelten Pfeil, zeigt die Vorgänge in einer explorativen statistischen Studie. Die rechte Seite der Abbildung, nach dem gestrichelten Pfeil, zeigt die Vorgänge in einer konfirmatorischen statistischen Studie.

Der Zweck der explorativen Studie besteht darin, Daten mit einer oder mehreren verschiedenen Techniken zu analysieren, um eine Hypothese zu untermauern. Der Datensatz kann neu definiert werden und/oder verschiedene Analysetechniken können wiederholt eingesetzt werden, um eine oder mehrere Hypothesen zu stützen. Die explorative Studie ist somit sehr flexibel gegenüber den Besonderheiten jeder wissenschaftlichen Fragestellung. Das wiederholte Testen von Hypothesen an einem Datensatz kann jedoch zu Problemen führen, die die statistischen Schlussfolgerungen untergraben. Dies ist auf die Mehrfachprüfung zurückzuführen, d. h. auf die Tatsache, dass ein statistischer Test mit mehreren unabhängigen Hypothesen mit größerer Wahrscheinlichkeit eine positive Signifikanz ergibt und dass die Wahrscheinlichkeit dafür mit der Prüfung weiterer Hypothesen steigt, selbst wenn die zugrunde liegenden Wahrscheinlichkeitsverteilungen identisch sind. Um irreführende statistische Ergebnisse zu vermeiden, wird die explorative Studie daher häufig mit einer konfirmatorischen Studie kombiniert.

Die Anforderungen an eine konfirmatorische Studie beruhen auf wesentlich strengeren statistischen Kriterien. Zum einen muss die Untersuchungshypothese, einschließlich der Signifikanzkriterien, vor der Datenerhebung und vor der Analyse festgelegt werden. Darüber hinaus muss der zu analysierende Datensatz ausschließlich zu diesem Zweck erhoben worden sein. Es ist statistisch nicht korrekt, den Datensatz aus der explorativen Studie in der konfirmatorischen Studie wiederzuverwenden, da dieser Datensatz von Natur aus die vorgeschlagene Hypothese begünstigen würde. Das Endergebnis der konfirmatorischen Studie ist eine abgelehnte oder akzeptierte Hypothese entsprechend den vorher festgelegten Kriterien.

Statistische Tests

Bei statistischen Tests wird die Wahrscheinlichkeit analysiert, dass ein beobachtetes Phänomen zufällig auftritt. Dies wird als Nullhypothese²⁸ bezeichnet. Wenn das beobachtete Phänomen gemäß der Nullhypothese selten ist, lautet die Schlussfolgerung, dass es unwahrscheinlich ist, dass die Nullhypothese gültig ist. Die Nullhypothese wird verworfen und die Wahrscheinlichkeit, dass die Alternativhypothese signifikant ist, wird akzeptiert.

Die geschätzte Wahrscheinlichkeit, dass das beobachtete Phänomen zufällig auftritt, wird als p-Wert bezeichnet. Der p-Wert wird in einem Bereich von 0 bis 1, oder äquivalent dazu, in Prozenteinheiten gemessen. Die statistischen Kriterien für eine konfirmatorische Studie umfassen einen Alpha-Cut-off, unter dem berechnete p-Werte Signifikanz für das beobachtete Phänomen anzeigen würden. Üblicherweise wird ein Alpha-Cut-off von 5 % verwendet, der jedoch an die gewünschten und notwendigen Kriterien angepasst werden muss, die für den jeweiligen Untersuchungsgegenstand spezifisch sind.

Es wurden zahlreiche Algorithmen zur Berechnung von p-Werten unter verschiedenen Annahmen und für unterschiedliche Zwecke entwickelt. Ein gängiger Algorithmus ist der Student's t-test. Der Student's t-Test wird verwendet, um einen p-Wert auf der Grundlage der Differenz der Mittelwerte zwischen zwei Datengruppen zu berechnen. Die Hauptannahme des Student's t-Tests ist, dass die beiden Datengruppen unabhängig sind und einer Normalverteilung entsprechen. Ein Vorteil des Student's t-Tests ist, dass er im Vergleich zu nichtparametrischen statistischen Tests²⁹ leistungsfähig ist. Ein nichtparametrischer Test, der dem Student's t-Test gleichwertig ist, kann einer der bekanntesten nichtparametrischen statistischen Tests sein: der Wilcoxon-Rangsummentest (manchmal auch Mann-Whitney-U-Test genannt; nicht zu verwechseln mit dem Wilcoxon-Signed-Rank-Test, der zum Vergleich zweier gepaarter Gruppen verwendet wird). Nichtparametrische statistische Tests, wie der Wilcoxon-Rangsummentest, haben gegenüber parametrischen statistischen Tests, wie dem Student's t-Test, den Vorteil, dass sie nicht von Vorannahmen über die Verteilungen der Datensätze abhängen. Ein Kolmogorov-Smirnov-Test auf Normalverteilung kann verwendet werden, um zu entscheiden, ob der Student's t-Test oder einer der nichtparametrischen Tests angewendet werden soll

Neben der Wahl des Algorithmus für p-Wert-Berechnung, können Datensätze, die in den Algorithmus zur Berechnung des p-Wertes eingespeist werden, manipuliert werden, um die Beobachtung der gewünschten Eigenschaften im Datensatz zu erleichtern. Die Kombination der Schritte zur Manipulation der Rohdaten und der Wahl des Algorithmus zur Berechnung des p-Wertes ist Teil des Aufbaus eines Hypothesenmodells.

Der Aufbau von Hypothesenmodellen in der explorativen Phase einer statistischen Analyse bietet ein hohes Maß an Freiheit und ist ein wichtiger Teil der wissenschaftlichen Untersuchung. Eine Hypothese wird jedoch niemals durch einen wissenschaftlichen, statistischen Ansatz bewiesen. Ein korrekter wissenschaftlicher Ansatz besteht darin, eine Nullhypothese zu formulieren, einen unabhängigen (vorzugsweise einen neu erhobenen) Datensatz zu verwenden und die Nullhypothese gemäß dem Flussdiagramm für konfirmatorische Studien (Abbildung 10.10) zu akzeptieren oder zu verwerfen.

Visualisierungstechniken für univariate Analysen

So wie es viele Analysemethoden gibt, gibt es auch viele Datenvisualisierungstechniken, aus denen man wählen kann. Für die univariate Datenanalyse ist ein einfaches Balkendiagramm mit zugehörigen Fehlerbalken eine geeignete Visualisierungstechnik. Obwohl es sich hierbei um eine gängige und einfache Visualisierungstechnik handelt, gibt es einige Punkte, die hervorgehoben werden sollten. Erstens können die Fehlerbalken verschiedene Quellen der Variabilität veranschaulichen: die inhärente Variabilität der Daten (die Standardabweichung, SD) oder die Genauigkeit, mit der der Mittelwert bestimmt wurde. Zweitens kann die Genauigkeit, mit der der Mittelwert bestimmt wurde, auf verschiedene Weise dargestellt werden, aber sie hängt letztendlich von einer Kombination der inhärenten Variabilität der Daten zusammen mit der Anzahl der Stichproben (N) ab und wird in ihrer Rohform als Standardfehler des Mittelwerts (SEM, Gleichung 1) bezeichnet:

Gleichung 1. SEM

Das SEM ist jedoch kein sehr intuitives Maß, und es ist nicht einfach, SEMs aus verschiedenen Experimenten auf sinnvolle Weise zu vergleichen. Ein beliebteres Mittel, um die Genauigkeit des geschätzten Mittelwerts zu veranschaulichen und die statistische Signifikanz grafisch darzustellen, ist das Konfidenzintervall (CI,Gleichung 2):

Gleichung 10-2. Cl

Das Vorhandensein des SEM ist in der Gleichung für das Konfidenzintervall als das Verhältnis zwischen der Standardabweichung (SD) und der Quadratwurzel der Anzahl der Stichproben (N) zu erkennen, und somit ist es offensichtlich, dass das Konfidenzintervall auf dem SEM basiert. Die untere Grenze des Konfidenzintervalls wird konstruiert, indem der SEM multipliziert mit einem Perzentil einer t-Verteilung vom Mittelwert subtrahiert wird. Die obere Grenze des Konfidenzintervalls wird durch Addition des SEM, multipliziert mit einem Perzentil einer t-Verteilung, zum Mittelwert gebildet. Das Konfidenzniveau des Konfidenzintervalls wird durch das Konfidenzniveau festgelegt, das mit dem kritischen Wert t* verbunden ist; in der Regel ein Konfidenzniveau von 95 %.

Abbildung 10.11 zeigt ein Balkendiagramm mit Fehlerbalken, die das 95 %-Konfidenzintervall innerhalb jeder Versuchsgruppe angeben und die Unsicherheit hervorheben, die mit der mittleren Schätzung für ein Beispiel der Genexpression in Proben aus verschiedenen Organen nach der Behandlung mit mehreren Medikamentendosen verbunden ist. Darüber hinaus werden die Werte für die statistische Signifikanz des t-Tests für den Unterschied in der Genexpression zwischen den Kontrollproben und jeder der drei verschiedenen Proben, die auf unterschiedliche Arzneimitteldosen reagiert haben, mit einem Sternchen gekennzeichnet. Üblicherweise entspricht ein Sternchen einemp-Wert unter 0,05, zwei Sternchen einemp-Wert unter 0,01 und drei Sternchen einemp-Wert unter 0,001.

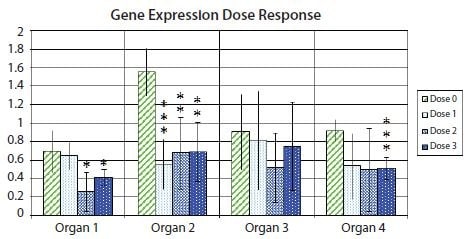
Abbildung 10.11. Fold change (log2) Expression eines Gens von Interesse relativ zu einem Paar von Referenzgenen, bezogen auf die Expression in der Probe mit der niedrigsten Expression innerhalb jedes Organtyps. Die Balkenhöhen zeigen die mittlere Expression des Gens in mehreren Proben in Gruppen von nicht behandelten (Dosis 0) Proben oder Proben, die mit einer von drei verschiedenen Medikamentendosen (Dosis 1, Dosis 2 und Dosis 3) behandelt wurden. Die Fehlerbalken zeigen 95%ige Konfidenzintervallschätzungen der mittleren Ausprägungen an. Ein Sternchen bedeutet einen statistisch signifikanten Unterschied zwischen den Mittelwerten eines behandelten Probensatzes im Vergleich zum Mittelwert des nicht behandelten Probensatzes auf 5%; zwei Sternchen bedeuten einen statistisch signifikanten Unterschied auf 1%; drei Sternchen bedeuten einen statistisch signifikanten Unterschied auf 0,1%.

Da die Sternchenschreibweise den absoluten Wert von p verbirgt, wird oft empfohlen, eine Tabelle mit den absoluten Werten von p, wie in dem Beispiel in Tabelle 10.5 gezeigt. Ein Grund dafür ist, dass ein p-Wert von beispielsweise 0,032 nur wenig "signifikanter" ist als ein p-Wert von 0,055. Grenzfälle wie dieser können zu einer gewissen Verwirrung führen, wenn es darum geht, zu entscheiden, welcher Grenzwert bei der Einstufung von Daten als signifikant verwendet werden soll. In realistischen Fällen könnte ein p-Wert von 0,051 ebenso signifikant sein wie ein p-Wert von 0,049 sein, doch ein strenger (wenn auch grundsätzlich willkürlicher) Grenzwert von 0,05 würde das eine als signifikant einstufen und das andere nicht.

Tabelle 10.5Signifikanzschätzungen der Mittelwertdifferenz. Die Mittelwerte der Expression eines Gens von Interesse aus einem behandelten Probensatz werden mit den Mittelwerten der unbehandelten Proben verglichen und relativ zu den Expressionsdaten für zwei Referenzgene ausgedrückt. Die Daten werden relativ zu der Probe mit der niedrigsten Expression für jeden Organtyp dargestellt (Daten in Abbildung 10.12). Der Student's t-Test wurde zur Ermittlung der p-Werte verwendet.

Genexpression p-Werte
	Organ 1	Organ 2	Organ 3	Organ 4
Dosis 1 vs Dosis 0	0.70274	0.00034***	0.78194	0.05551
Dosis 2 vs. Dosis 0	0.01379*	0.00295**	0.20956	0.07582
Dosis 3 vs. Dosis 0	0.03180*	0.00157**	0.61582	0,00075***

Es gibt jedoch eine Variante der Balkendiagramm-Darstellung, die sich das Konfidenzintervall der Differenz zwischen den Mittelwerten zunutze macht, um viele, wenn nicht sogar alle Nachteile der traditionellen Balkendiagramme²⁴ zu vermeiden. Mit dem Konfidenzintervall der Differenz zwischen den Mittelwerten ist es möglich, die statistische Signifikanz mit zugehörigen Fehlerbalken direkt abzuschätzen und gleichzeitig die biologische Effektgröße und die Datenvariabilität hervorzuheben.Abbildung 10.12 zeigt die Variante mit dem Konfidenzintervall der Differenz zwischen den Mittelwerten der in Abbildung 10.11 verwendeten Daten. Man beachte, dass Konfidenzintervalle, die nicht die Differenz zwischen den Mittelwerten von Null umfassen, signifikanten Ergebnissen auf dem Konfidenzniveau entsprechen, das dem Grenzwert für den p-Wert entspricht (5 % in Abbildung 10.11 und Tabelle 10.5).

Abbildung 10.12. Balkendiagramm, das die Differenz zwischen den Mittelwerten des unbehandelten Probensatzes (Dosis 0) und einem der behandelten Probensätze (Dosis 1, Dosis 2 oder Dosis 3) im Datensatz aus Abbildung 10.11 zeigt. Die Fehlerbalken zeigen das Konfidenzintervall der Differenz zwischen den Mittelwerten. Fehlerbalken, die die x-Achse nicht kreuzen, zeigen an, dass der entsprechende Mittelwertvergleich in einem t-Test mit 5 % statistisch signifikant ist. PCR Technology, Current Innovations-3rd ed. by Taylor and Francis Group LLC Books. Nachdruck mit Genehmigung von Taylor and Francis Group LLC Books im Format der Wiederverwendung in einem Buch/E-Book über das Copyright Clearance Center.

Multivariate Daten sind Daten, die zu mehreren Variablen für jede Stichprobeneinheit erhoben werden. Die in den Abbildungen 10.11 und 10.12 verwendeten Daten sind insofern multivariat, als sie von Variablen wie Dosis und Organtyp abhängen. Die statistischen Analysen in den Abbildungen 10.11 und 10.12 sind jedoch insofern univariat, als jede Darstellung (Balken) nur eine Variable, die Genexpression, in Relation zu festen Maßen der anderen Variablen darstellt. Für multivariate Datenanalyseverfahren sind hierarchisches Clustering und Hauptkomponentenanalyse gute Optionen für die Datendarstellung.

Hierarchisches Clustering

Eine der einfachsten und nützlichsten Methoden zur Charakterisierung von Daten ist die Darstellung der Daten in einem Scatterplot (z. B. die Darstellung der gemessenen C_q -Werte eines Gens gegen die entsprechenden C_q -Werte eines anderen Gens für eine Reihe von biologischen Proben in einem 2D-Diagramm). Ein- oder zweidimensionale Darstellungen sind für das menschliche Auge leicht zu erkennen. Auch dreidimensionale Darstellungen sind mit geeigneten Werkzeugen möglich, aber höherdimensionale Darstellungen sind wesentlich schwieriger zu visualisieren. Bei explorativen Studien ist der Datensatz jedoch von Natur aus mehrdimensional und Streudiagramme ganzer Datensätze können daher unpraktisch sein. In einem qPCR-Datensatz können beispielsweise mehrere Gene und/oder mehrere Arten von biologischen Proben vertreten sein.

Eine beliebte, alternative Methode zur Charakterisierung und Visualisierung von Daten aus explorativen Studien ist die Analyse von Abstandsmaßen zwischen Datenpunkten im Streudiagramm. Es gibt verschiedene Abstandsmaße, darunter euklidische, Manhattan- und Pearson-Korrelationen. Mit der entsprechenden Rechenleistung ist es einfach, Abstände zu berechnen, selbst für mehrdimensionale Daten mit einer viel höheren Dimensionalität als drei Dimensionen. Beim agglomerativen hierarchischen Clustering wird der folgende iterative Prozess durchgeführt: 1) Suche nach den beiden nächstgelegenen Objekten und Zusammenschluss zu einem Cluster; 2) Definition des neuen Clusters als neues Objekt durch eine Clustermethode; 3) Wiederholung von 1), bis alle Objekte zu Clustern³⁰ zusammengefasst sind. Zu den alternativen Clustermethoden gehören die Ward-Methode, die Einfachverknüpfung und die Durchschnittsverknüpfung³¹. Ein Dendrogramm wird häufig verwendet, um die Ergebnisse des hierarchischen Clustering zu visualisieren.

Die Interpretation von hierarchischen Clustering-Dendrogrammen von qPCR-Daten führt häufig zu Schlussfolgerungen über Ähnlichkeiten im Genexpressionsprofil. In einer explorativen Studie können diese Ähnlichkeiten dann dazu verwendet werden, Hypothesen über die Genexpressions-Koregulation zu formulieren, die in anschließenden Bestätigungsstudien bestätigt oder verworfen werden können. Zu den Vorteilen der hierarchischen Cluster-Dendrogramme gehört die Klarheit, mit der die Ähnlichkeitsbeziehungen visualisiert werden. Andererseits kann die starke Betonung von Ähnlichkeitsmaßen als Einschränkung bei der Formulierung von Hypothesen empfunden werden, da ähnliche Expressionsprofile redundante Attribute in Hypothesen sein können. Es kann von größerem Wert sein, Gruppen von Expressionsprofilen zu identifizieren, die sich in einer bestimmten Kombination ergänzen, um die gewünschte Hypothese zu beantworten.

Principal Component Analysis

Eine weitere beliebte, alternative Methode zur Charakterisierung und Visualisierung von Daten aus explorativen Studien besteht darin, die im gesamten, mehrdimensionalen Datensatz enthaltenen Informationen zu nutzen, die gewünschten Eigenschaften auszuwählen und sie auf ein niedriger dimensioniertes Streudiagramm zu projizieren, z. B. ein 2D- oder 3D-Diagramm. Dies kann mit Hilfe der Hauptkomponentenanalyse (PCA)^{32,33,34, 35} erreicht werden. Dabei wird das ursprüngliche Koordinatensystem des Datensatzes (d. h. die mittels qPCR gemessenen Expressionsprofile) in einen neuen mehrdimensionalen Raum transformiert, in dem neue Variablen (Hauptkomponenten: PC oder Faktoren) konstruiert werden. Jeder PC ist eine Linearkombination der Fächer im ursprünglichen Datensatz. Nach mathematischer Definition werden die PC in der Reihenfolge ihrer Bedeutung extrahiert. Das bedeutet, dass der erste PC den größten Teil der in den Daten vorhandenen Informationen (Varianz) erklärt, der zweite weniger und so weiter. Daher können die ersten zwei oder drei PC-Koordinaten (als Scores bezeichnet) verwendet werden, um eine Projektion des gesamten Datensatzes auf eine kleine Dimension zu erhalten, die sich für die Visualisierung in einer 2D- oder 3D-Darstellung eignet. Durch die Verwendung der ersten zwei oder drei PC zur Darstellung erhält man die Projektion, die die größte Variabilität im Datensatz berücksichtigt. Es ist davon auszugehen, dass die durch die Versuchsbedingungen bedingte Varianz systematisch ist, während man davon ausgeht, dass störende Varianz zufällig ist, so dass diese Darstellung unter geeigneten Bedingungen erwünscht sein kann.

Wie bereits für das hierarchische Clustering festgestellt, führt die Interpretation der qPCR-PCA häufig zu Schlussfolgerungen über die Ähnlichkeit der Genexpressionsprofile. Obwohl PCA und hierarchisches Clustering komplementäre Einblicke in Ko-Regulationsmuster der Genexpression liefern können, konzentrieren sich beide Techniken auf Ähnlichkeiten der Genexpressionsprofile. Dies schränkt die Arten von Hypothesen ein, die in explorativen Studien mit diesen Techniken allein gefunden werden können. Um die Reichweite der in explorativen Studien generierten Hypothesen zu erweitern, wurde kürzlich ein hypothesengesteuerter Ansatz für die multivariate Analyse vorgeschlagen²⁴. Hypothesengesteuerte, maßgeschneiderte Algorithmen können biologisch relevante Hypothesen identifizieren, die andernfalls von den üblicherweise verwendeten Techniken zur multivariaten Datenanalyse übersehen werden könnten.

Materialien

Bitte entschuldigen Sie, es ist ein unerwarteter Fehler aufgetreten

Response not successful: Received status code 500

1. Bustin SA, Benes V, Garson JA, Hellemans J, Huggett J, Kubista M, Mueller R, Nolan T, Pfaffl MW, Shipley GL, et al. 2009. The MIQE Guidelines: Minimum Information for Publication of Quantitative Real-Time PCR Experiments. 55(4):611-622. https://doi.org/10.1373/clinchem.2008.112797

2. Guescini M, Sisti D, Rocchi MB, Stocchi L, Stocchi V. 2008. A new real-time PCR method to overcome significant quantitative inaccuracy due to slight amplification inhibition. BMC Bioinformatics. 9(1): https://doi.org/10.1186/1471-2105-9-326

3. Rutledge RG, Stewart D. 2008. Critical evaluation of methods used to determine amplification efficiency refutes the exponential character of real-time PCR. BMC Mol Biol. 9(1):96. https://doi.org/10.1186/1471-2199-9-96

4. Rutledge RG, Stewart D. 2008. A kinetic-based sigmoidal model for the polymerase chain reaction and its application to high-capacity absolute quantitative real-time PCR. BMC Biotechnology. 8(1):47. https://doi.org/10.1186/1472-6750-8-47

5. Livak KJ, Schmittgen TD. 2001. Analysis of Relative Gene Expression Data Using Real-Time Quantitative PCR and the 2???CT Method. Methods. 25(4):402-408. https://doi.org/10.1006/meth.2001.1262

6. Pfaffl MW. 2001. A new mathematical model for relative quantification in real-time RT-PCR. 29(9):45e-45. https://doi.org/10.1093/nar/29.9.e45

7. Dheda K, Huggett JF, Bustin SA, Johnson MA, Rook G, Zumla A. 2004. Validation of housekeeping genes for normalizing RNA expression in real-time PCR. BioTechniques. 37(1):112-119. https://doi.org/10.2144/04371rr03

8. Dheda K, Huggett J, Chang J, Kim L, Bustin S, Johnson M, Rook G, Zumla A. 2005. The implications of using an inappropriate reference gene for real-time reverse transcription PCR data normalization. Analytical Biochemistry. 344(1):141-143. https://doi.org/10.1016/j.ab.2005.05.022

9. Vermeulen J, De Preter K, Lefever S, Nuytens J, De Vloed F, Derveaux S, Hellemans J, Speleman F, Vandesompele J. 2011. Measurable impact of RNA quality on gene expression results from quantitative PCR. 39(9):e63-e63. https://doi.org/10.1093/nar/gkr065

10. Ibberson D, Benes V, Muckenthaler MU, Castoldi M. 2009. RNA degradation compromises the reliability of microRNA expression profiling. BMC Biotechnology. 9(1):102. https://doi.org/10.1186/1472-6750-9-102

11. Huggett J, Dheda K, Bustin S, Zumla A. 2005. Real-time RT-PCR normalisation; strategies and considerations. Genes Immun. 6(4):279-284. https://doi.org/10.1038/sj.gene.6364190

12. Mitsuhashi M, Tomozawa S, Endo K, Shinagawa A. 2006. Quantification of mRNA in Whole Blood by Assessing Recovery of RNA and Efficiency of cDNA Synthesis. 52(4):634-642. https://doi.org/10.1373/clinchem.2005.048983

13. Whale AS, Huggett JF, Cowen S, Speirs V, Shaw J, Ellison S, Foy CA, Scott DJ. 2012. Comparison of microfluidic digital PCR and conventional quantitative PCR for measuring copy number variation. 40(11):e82-e82. https://doi.org/10.1093/nar/gks203

14. Vandesompele J, De Preter K, Pattyn F, Poppe B, Van Roy N, De Paepe A, Speleman F. 2002. Genome Biol. 3(7):research0034.1. https://doi.org/10.1186/gb-2002-3-7-research0034

15. Pfaffl MW. 2002. Relative expression software tool (REST(C)) for group-wise comparison and statistical analysis of relative expression results in real-time PCR. 30(9):36e-36. https://doi.org/10.1093/nar/30.9.e36

16. Pfaffl MW, Tichopad A, Prgomet C, Neuvians TP. 2004. Determination of stable housekeeping genes, differentially regulated target genes and sample integrity: BestKeeper ? Excel-based tool using pair-wise correlations. Biotechnology Letters. 26(6):509-515. https://doi.org/10.1023/b:bile.0000019559.84305.47

17. Andersen CL, Jensen JL, Ørntoft TF. 2004. Normalization of Real-Time Quantitative Reverse Transcription-PCR Data: A Model-Based Variance Estimation Approach to Identify Genes Suited for Normalization, Applied to Bladder and Colon Cancer Data Sets. Cancer Res. 64(15):5245-5250. https://doi.org/10.1158/0008-5472.can-04-0496

18. Eady JJ, Wortley GM, Wormstone YM, Hughes JC, Astley SB, Foxall RJ, Doleman JF, Elliott RM. 2005. Variation in gene expression profiles of peripheral blood mononuclear cells from healthy volunteers. Physiological Genomics. 22(3):402-411. https://doi.org/10.1152/physiolgenomics.00080.2005

19. Barnes MG, Grom AA, Griffin TA, Colbert RA, Thompson SD. 2010. Gene Expression Profiles from Peripheral Blood Mononuclear Cells Are Sensitive to Short Processing Delays. Biopreservation and Biobanking. 8(3):153-162. https://doi.org/10.1089/bio.2010.0009

20. Debey S, Schoenbeck U, Hellmich M, Gathof BS, Pillai R, Zander T, Schultze JL. 2004. Comparison of different isolation techniques prior gene expression profiling of blood derived cells: impact on physiological responses, on overall expression and the role of different cell types. Pharmacogenomics J. 4(3):193-207. https://doi.org/10.1038/sj.tpj.6500240

21. Mestdagh P, Van Vlierberghe P, De Weer A, Muth D, Westermann F, Speleman F, Vandesompele J. 2009. A novel and universal method for microRNA RT-qPCR data normalization. Genome Biol. 10(6):R64. https://doi.org/10.1186/gb-2009-10-6-r64

22. Mestdagh P, Derveaux S, Vandesompele J. 2012. Whole-Genome RT-qPCR MicroRNA Expression Profiling.121-130. https://doi.org/10.1007/978-1-61779-424-7_10

23. D?haene B, Mestdagh P, Hellemans J, Vandesompele J. 2012. miRNA Expression Profiling: From Reference Genes to Global Mean Normalization.261-272. https://doi.org/10.1007/978-1-61779-427-8_18

24. Nolan T, Bustin SA. 2013. PCR Technology: Current Innovations. 3. CRC Press.

25. Manly B. 1998. Randomization, Bootstrap and Monte Carlo Methods.. 2. Chapman Hall:

26. Kitchen RR, Kubista M, Tichopad A. 2010. Statistical aspects of quantitative real-time PCR experiment design. Methods. 50(4):231-236. https://doi.org/10.1016/j.ymeth.2010.01.025

27. Tichopad A, Kitchen R, Riedmaier I, Becker C, Sta?hlberg A, Kubista M. 2009. Design and Optimization of Reverse-Transcription Quantitative PCR Experiments. 55(10):1816-1823. https://doi.org/10.1373/clinchem.2009.126201

28. Fisher R. 1966. The design of experiments.. 8. Hafner: Edinburgh:

29. Motulsky H. 1995. Intuitive Biostatistics. New York: Oxford University Press.

30. Ward JH. 1963. Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association. 58(301):236-244. https://doi.org/10.1080/01621459.1963.10500845

31. Lance GN, Williams WT. 1967. A General Theory of Classificatory Sorting Strategies: 1. Hierarchical Systems. The Computer Journal. 9(4):373-380. https://doi.org/10.1093/comjnl/9.4.373

32. Rao C. 1964. The use and interpretation of principal components analysis in applied research..

33. Hotelling H. 1933. Analysis of a complex of statistical variables into principal components.. Journal of Educational Psychology. 24(6):417-441. https://doi.org/10.1037/h0071325

34. Pearson K. 1901. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 2(11):559-572. https://doi.org/10.1080/14786440109462720