Analisi dei dati PCR/qPCR

A Technical Guide to PCR Technologies

• Analisi qualitativa della PCR/qPCR
• Analisi dei dati della PCR
• Derivare valori di Cq accurati
• Impostazione della soglia
• Strategie di quantificazioneqPCR
• Quantificazione della curva standard
• Quantificazione relativa/comparativa
• Normalizzazione
• Selezione del gene di riferimento
• Analisi della stabilità del gene di riferimento
• Metodi alternativi di normalizzazione
• Analisi statistica e visualizzazione dei dati
• Tecniche di visualizzazione per l'analisi univariata
• Test statistici
• Clustering gerarchico
• Principal Component Analysis

Analisi dei dati qualitativi di PCR/qPCR

Dopo aver completato una PCR tradizionale, i dati vengono analizzati mediante risoluzione su gel di agarosio o, più recentemente, attraverso un sistema di elettroforesi capillare. Per alcune applicazioni, viene eseguita una qPCR con i dati end-point utilizzati per l'analisi, ad esempio per la genotipizzazione degli SNP. In ogni caso, i dati end-point forniscono un'analisi qualitativa dopo che la PCR ha raggiunto la fase di plateau. In alcuni casi, può essere possibile analizzare i dati end-point per effettuare un'analisi semi-quantitativa della resa della PCR, ma le misurazioni quantitative sono più spesso effettuate utilizzando la qPCR e l'analisi dei valori del ciclo di quantificazione (C_q)¹ valori.

Analisi dei dati qPCR

In questa guida sono stati evidenziati i fattori che contribuiscono alle variazioni nella misurazione degli acidi nucleici mediante PCR o qPCR. Ognuno di questi fattori deve essere ottimizzato per ottenere un saggio che fornisca il valore più vicino possibile alla quantità effettiva di gene (target) nella reazione. Il risultato di questi processi è la generazione di una serie di valori C_q  per ciascun target in ogni campione. In questo capitolo viene presentato il processo di derivazione e analisi di questi valori C_q per fornire dati affidabili che rappresentino la storia biologica.

Derivare valori C_q accurati

Correzione della linea di base

Un valore C_q viene determinato per ogni target in ogni campione. Diversi pacchetti di analisi, associati a diversi strumenti, hanno approcci alternativi per la determinazione del C_q  (e utilizzano anche nomi alternativi, ad esempio C_t, C_p, take off point). Non è compito di questa guida approfondire i dettagli di tutti questi algoritmi. Tuttavia, le misurazioni qPCR basate sulle curve di amplificazione sono sensibili alla fluorescenza di fondo. La fluorescenza di fondo può essere causata da una serie di fattori, tra cui la scelta del materiale plastico, la fluorescenza residua della sonda che non viene estinta, la luce che fuoriesce dal pozzetto del campione e le differenze nella rilevazione ottica per un determinato pozzetto della piastra di microtitolazione. Nei saggi ben progettati, il fondo è basso rispetto al segnale amplificato. Tuttavia, la variazione del segnale di fondo può ostacolare il confronto quantitativo di campioni diversi. Pertanto, è importante correggere le variazioni della fluorescenza di fondo che causano differenze nella linea di base (Figura 10.1).

Figura 10.1 I componenti dei grafici di amplificazione. Questo grafico mostra l'aumento della fluorescenza con il numero di cicli per diversi campioni. La soglia è impostata al di sopra del limite di rilevazione, ma ben al di sotto della fase di plateau durante la quale il tasso di amplificazione rallenta.

Un approccio comune consiste nell'utilizzare l'intensità della fluorescenza durante i primi cicli, ad esempio tra i cicli da 5 a 15, per identificare una componente costante e lineare della fluorescenza di fondo. Questa viene poi definita come fondo o linea di base per il grafico di amplificazione. A causa degli effetti transitori, è consigliabile evitare i primi cicli (ad esempio, i cicli da 1 a 5) per la definizione della linea di base, perché spesso presentano artefatti di stabilizzazione della reazione. Più cicli vengono utilizzati per la correzione della linea di base, migliore è l'accuratezza potenziale della componente lineare delle variazioni della linea di base. Molti pacchetti software per strumenti consentono di impostare manualmente i cicli da considerare per la definizione della linea di base. L'utente dovrebbe esplorare queste funzioni e resistere alla tentazione di accettare le impostazioni predefinite.

Un esempio dell'effetto dell'impostazione della linea di base è mostrato nella Figura 10.1. Come si può notare, i valori di C_q e la forma apparente del grafico di amplificazione sono influenzati da un'accurata impostazione della linea di base. Nell'esempio, la linea di base per la curva contrassegnata con C3 è stata regolata manualmente in modo errato, in modo che i cicli della linea di base siano calcolati dai dati dei cicli da 5 a 31. Ciò provoca un'immersione della curva nella parte bassa del grafico. Questo fa sì che la curva si abbassi al livello zero della linea di base (Figura 10.2A) con un C_q di 28,80. Per correggere questo problema, si visualizzano i dati grezzi, R, e si identifica l'ultimo ciclo del fondo lineare (l'ultimo ciclo prima dell'amplificazione). Nella Figura 10.2B, si può notare che si tratta del ciclo 22. La linea di base è impostata correttamente. La linea di base viene impostata correttamente a zero tra il ciclo 5 e il ciclo 22 (Figura 10.2C) e il grafico di amplificazione viene quindi corretto (Figura 10.2D). Il C_q corretto è 26,12. Si noti quindi che c'era una differenza sostanziale tra i valori di C_q con le impostazioni di baseline errate e corrette, a dimostrazione del fatto che l'impostazione della baseline corretta è una componente importante dell'analisi dei dati.

Figura 10.2A-B. A) Esempio tipico di caduta dei dati al di sotto della lettura di fluorescenza normalizzata zero quando l'impostazione della linea di base non è corretta (grafico di amplificazione blu). B) Dati grezzi degli stessi grafici di amplificazione che mostrano il limite della linea di base lineare e che i dati non sono errati.

Figura 10.2C-D. C) I limiti dell'inizio e della fine della linea di base sono definiti utilizzando le impostazioni software appropriate. D) L'applicazione dell'impostazione corretta della linea di base produce dati di buona qualità.

Impostazione della soglia

Anche se alcuni ricercatori sostengono la necessità di mappare i singoli plot di amplificazione per stimare l'efficienza di amplificazione e le quantità target nei campioni misurati^2,3,4, l'approccio originale e più comune per ricavare il C_q è quello di utilizzare una soglia. Il principio alla base del metodo della soglia è che, per poter visualizzare il segnale fluorescente associato all'amplificazione qPCR, il segnale deve aumentare in modo da superare il limite di rilevamento dello strumento (e quindi la linea di base; Figura 10.1). Il numero di cicli necessari perché ciò avvenga è proporzionale al numero iniziale di copie del target nel campione. Pertanto, sono necessari più cicli perché il segnale aumenti al di sopra della linea di base se il numero di copie originale è basso e meno cicli se il numero di copie è alto. Poiché la linea di base è impostata al limite di rilevamento del sistema, le misurazioni alla linea di base sarebbero molto imprecise. Pertanto, piuttosto che misurare all'intensità di fluorescenza minima che il sistema è in grado di rilevare, si seleziona una fluorescenza più alta e si introduce una soglia artificiale.

La selezione dell'intensità della soglia richiede il rispetto di alcuni principi fondamentali. È importante che la soglia sia impostata a un'intensità fissa per un determinato target e per tutti i campioni da confrontare. Se il numero di campioni è troppo elevato per essere inserito in una singola piastra, è necessario adottare uno schema di calibrazione interpiastra, ad esempio includendo un controllo replicato che funga da controllo interpiastra o una diluizione seriale della curva standard. In teoria, la soglia può essere impostata in qualsiasi punto della fase log-lineare della curva di amplificazione. Tuttavia, in pratica, la fase log-lineare dell'amplificazione può essere disturbata dalla deriva della linea di base della fluorescenza di fondo, dalla fase di plateau o da differenze nell'efficienza del saggio e quindi dal gradiente della trama di amplificazione a cicli più elevati. Si raccomanda di impostare la soglia come segue:

• Sufficientemente al di sopra della linea di base della fluorescenza di fondo per essere sicuri di evitare che il grafico di amplificazione attraversi prematuramente la soglia a causa della fluorescenza di fondo.
• Nella fase log del grafico di amplificazione, dove non è influenzato dalla fase di plateau (questo è più facilmente visibile visualizzando i grafici di amplificazione su una vista log, Figura 10.3A).
• In una posizione in cui le fasi logiche di tutti i diagrammi di amplificazione sono parallele.

Il processo di impostazione della soglia è dimostrato nella Figura 10.3. In Figura 10.3A, i grafici di amplificazione sono visualizzati su una scala log dell'asse Y, fornendo così un'espansione visiva della fase log dell'amplificazione e presentandola come una porzione lineare del grafico di amplificazione. La soglia viene impostata all'intensità di fluorescenza più alta (riferita all'asse Y) che si trova all'interno di questa fase log e in cui tutti i grafici di amplificazione sono paralleli. La scala viene quindi riportata alla vista lineare (Figura 10.3B) mostrando l'impostazione più alta che soddisfa i requisiti di impostazione della soglia. In alternativa, la soglia può essere impostata all'estremità inferiore di questa fase log (Figure 10.3C e 10.3D). Finché le fasi logiche dei diagrammi di amplificazione sono parallele, il ΔC_q tra i campioni non è influenzato dall'impostazione della soglia.

Figura 10.3 L'impostazione della soglia influenza il Cq assoluto registrato e può influenzare il ΔCq tra i campioni. A). Utilizzando un diagramma logico/lineare dei dati, la soglia viene impostata in corrispondenza dell'intensità di fluorescenza più elevata, ma dove i diagrammi di amplificazione mostrano fasi logiche parallele. B). L'impostazione della soglia viene mantenuta da A) e viene visualizzata sul grafico lineare vs lineare. C). Utilizzando un grafico log vs. lineare dei dati, la soglia viene impostata all'intensità di fluorescenza più bassa, ma dove i grafici di amplificazione mostrano fasi logiche parallele. D). L'impostazione della soglia viene mantenuta da C) e viene visualizzata sul grafico lineare vs lineare. In ogni caso, i valori ΔCq tra i campioni sono gli stessi.

Il requisito di un'impostazione della soglia in una posizione in cui le fasi log-lineari delle trame di amplificazione sono parallele diventa più pertinente quando si includono nell'analisi dati a cicli più elevati. La procedura di impostazione della soglia descritta per i dati in Figura 10.3 è stata ripetuta su un set di dati con C_q più elevato e i risultati sono stati presentati in Figura 10.4. I dati C_q risultanti nella Tabella 10.1 servono a illustrare la variabilità dei valori di C_q e, soprattutto, di ΔC_q per tre trame di amplificazione con tre impostazioni di soglia (Figura 10.4). I valori ΔC_q e quindi la stima della quantità relativa di target in ciascun campione dipendono fortemente dall'impostazione della soglia (Figura 10.4) perché i diagrammi di amplificazione non sono paralleli.

Tabella 10.1Dipendenza dei valori relativi di Cq dalla posizione dell'impostazione della soglia.

Soglia 1 valore Cq valore	ΔCq (1)	Soglia 2 Valore Cq	ΔCq (2)	Soglia 3 Valore Cq	ΔCq (3)
30.67		28,77		32.33
37,38	6,71	35,17	6.4	39,31	6,98
35,03	4,36	32.99	4,22	36,88	4,55

Figura 10.4. L'analisi eseguita e dimostrata nella Figura 10.3 è stata ripetuta utilizzando un altro set di dati. In questo caso, i diagrammi di amplificazione non sono paralleli a causa di una differenza di efficienza della reazione ad alta Cq. Le impostazioni più basse per A) e B) risultano in valori di ΔCq diversi rispetto alle impostazioni più alte per C) e D) (riassunte nella Tabella 10.1).

Strategie di quantificazione della qPCR

Un'accurata impostazione della linea di base e della soglia è indispensabile per una quantificazione affidabile. Dopo aver impostato ciascuno di questi valori, viene generato un valore C_q che viene utilizzato come base per la quantificazione. La quantità di target in un dato campione viene quindi determinata utilizzando una curva standard o una quantificazione relativa/comparativa.

Quantificazione con curva standard

Come suggerisce il nome, la quantificazione con curva standard richiede l'uso di una curva standard per determinare le quantità di target nei campioni in esame. Tutte le quantità determinate per i campioni sono quindi relative alla quantità assegnata alla curva standard. Ciò richiede l'esecuzione di standard esterni aggiuntivi accanto a ogni serie di reazioni dei campioni. La scelta del materiale per la curva standard è importante per eliminare le potenziali differenze di quantificazione dovute alle differenze di efficienza del dosaggio nei campioni e negli standard. I siti di legame dei primer degli standard esterni devono essere uguali a quelli del target, contenere sequenze uguali a quelle del target, avere una complessità simile ed essere gestiti nel modo più simile possibile. Pertanto, quando si misura la concentrazione di un target nel cDNA, è preferibile misurare lo stesso cDNA in una diluizione seriale di un campione di controllo. Tuttavia, per alcuni studi vi sono ragioni pratiche che lo impediscono, per cui è importante riprodurre le condizioni del campione il più fedelmente possibile, ad esempio aggiungendo gDNA di una specie non correlata alla specie in esame, a un oligonucleotide standard artificiale o a un plasmide linearizzato che trasporta la sequenza standard. Una volta identificato un costrutto o un amplicone adatto, viene generata una curva standard di diluizioni seriali. Il C_q per il target viene determinato per ciascuno degli standard e tracciato rispetto alla concentrazione o al fattore di concentrazione/diluizione relativa su una scala log. Si ottiene così una curva standard che viene poi utilizzata per determinare le concentrazioni dei campioni in esame confrontando i valori di C_q derivati dall'amplificazione dei campioni sconosciuti. Quando si utilizza una curva standard per la quantificazione, l'impostazione della soglia deve essere mantenuta costante per la determinazione di C_q per lo standard e per i campioni sulla stessa piastra. La soglia può variare da una piastra all'altra.

Quantificazione relativa/comparativa

La quantificazione relativa o comparativa utilizza la differenza di C_q come determinante delle differenze di concentrazione della sequenza target in campioni diversi. Invece di misurare le quantità di target per campione, come nel caso del metodo della curva standard, questo metodo porta a una serie di dati che mostrano le variazioni di fold tra i campioni.

Nella forma originale di questo approccio⁵, l'efficienza di tutti i test è stata assunta pari al 100%, il che ha portato all'ipotesi che un C_q di 1 (ΔC_q = 1) fosse il risultato di una differenza di 2 volte nel target. Per determinare una variazione di ripiegamento nel target o nel gene di interesse (GOI), i dati devono essere riferiti anche a un controllo di carico (gene di riferimento, ref; si veda quanto segue per una discussione sulla normalizzazione dei dati).

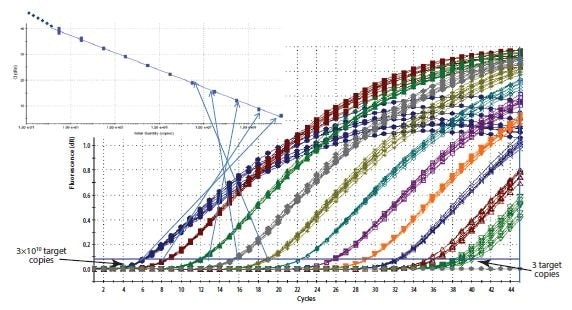
Figura 10.5. Costruzione di una curva standard. La Cq registrata per ciascun campione di una serie di diluizioni viene tracciata su una scala logaritmica rispetto alla concentrazione relativa.

Nella equazione 1, il rapporto del GOI, dopo la correzione al gene ref, in 2 campioni (A rispetto a B) è misurato come: 2 (assumendo reazioni efficienti al 100%) elevato alla potenza delle differenze nei valori C_q per il GOI diviso per 2 elevato alla potenza delle differenze nei valori C_q per il gene ref

Equazione 1. Modello di quantificazione relativa originale (Livak).

Come illustrato in Assay Optimization and Validation, le efficienze delle reazioni variano notevolmente e questo può avere un forte impatto sui dati. Pertanto, le ipotesi dell'Equazione 1 sono state affrontate (Equazione 2)⁶, in modo da poter incorporare nelle analisi le differenze nelle efficienze di reazione. In questo caso, il fattore di amplificazione 2 è sostituito dall'efficienza effettiva della PCR (determinata da un'analisi della curva standard; vedere Ottimizzazione e validazione del saggio).

Equazione 2. Modello di quantificazione relativa adattato all'efficienza (Pfaffl)

Come esempio di utilizzo del modello di quantificazione relativa adattato all'efficienza (Equazione 2), una serie di valori di C_q sono presentati nella Tabella 10.2. L'efficienza per il GOI è pari a 1,8 e per il gene ref a 1,94.

Tabella 10.2Esempio di lavoro per calcolare la variazione di ripiegamento (rapporto) utilizzando le differenze di Cq.

Soglia 1	Cq GOI	ΔCq GOI	EΔCq GOI	Cq Ref	ΔCq Rif	EΔCq Rif	EΔCq GOI EΔCq Ref
1	34			18			<
2	26	8	110.2	17	1	1,94	56,8

Questo è un esempio molto semplice di uno studio che richiede di misurare la differenza di ripiegamento tra un gene in due campioni e dopo la normalizzazione a un singolo gene di riferimento. Il rapporto mostra la variazione di ripiegamento del GOI nel campione 2 rispetto al campione 1, dopo la correzione al singolo gene di riferimento. Tuttavia, è diventato evidente che la selezione di un singolo gene di riferimento adatto è spesso impossibile e, pertanto, sono stati proposti approcci più sofisticati per la normalizzazione.

Normalization

L'obiettivo principale della maggior parte degli esperimenti basati sulla PCR è quello di rispondere alla domanda di base se il target è presente nel campione (unknown, UNK). Al livello più semplice, la risposta si ottiene eseguendo un gel ed esaminando i frammenti per verificare la presenza o l'assenza del GOI desiderato. Quando il frammento è presente, la conferma della dimensione del frammento rassicura su un risultato positivo. Tuttavia, quando è assente, esiste la possibilità di un risultato falso negativo. Per questo motivo, è fondamentale ripetere il test ed eseguire almeno un'ulteriore PCR che serva come controllo di carico e PCR positiva. Il saggio universale di controllo dell'inibizione, SPUD (vedi Purificazione del campione e valutazione della qualità), può essere utilizzato a sostegno della fiducia in un risultato negativo. Un approccio alternativo consiste nell'eseguire un saggio specifico per uno o più geni di riferimento. Tradizionalmente, i saggi PCR che rilevano i geni di riferimento, GAPDH, 18S RNA ribosomiale o β actina, vengono eseguiti insieme a quelli per le GOI e i frammenti risultanti vengono visualizzati su un gel. La GAPDH, l'RNA ribosomiale 18S e la β actina sono espressi costitutivamente e sono stati quindi utilizzati come controlli di carico nelle analisi semiquantitative. Tuttavia, è apparso subito evidente che questi geni non sono espressi in modo ubiquitario alla stessa concentrazione in tutte le cellule, indipendentemente dal disegno sperimentale. Pertanto, è nata l'esigenza di un riferimento stabile quando l'obiettivo era quello di misurare le concentrazioni relative di acidi nucleici, di solito cDNA ma anche gDNA quando, ad esempio, si esamina la variazione del numero di copie di un gene.

La normalizzazione è il processo di correzione delle misurazioni tecniche rispetto a un riferimento stabile, al fine di esaminare la vera variazione biologica. Esistono molti metodi per normalizzare le differenze tecniche, il che significa che l'approccio appropriato per l'esperimento specifico deve essere selezionato e convalidato⁷. È fondamentale riconoscere che l'adozione di tecniche di normalizzazione inadeguate può essere più dannosa per il processo analitico complessivo che non normalizzare affatto⁸.

L'effetto della qualità del campione sulla normalizzazione del saggio

L'effetto dell'integrità e della purezza del campione sulle misurazioni della quantità target mediante qPCR e RT-qPCR è stato discusso a lungo (Purificazione del campione e valutazione della qualità, Controllo della qualità del campione e Trascrizione inversa, Trascrizione inversa). È stato dimostrato che gli inibitori presenti nel campione e la degradazione dell'RNA hanno un effetto diverso sulla misurazione di un determinato target⁹. Gli inibitori influiscono sulla misurazione di qualsiasi target, ma in misura diversa, a seconda del disegno del saggio. La degradazione dell'RNA totale influisce sulla misurazione dell'mRNA e del miRNA¹⁰, ma anche in questo caso dipende fortemente dal disegno sperimentale complessivo. Pertanto, è fondamentale considerare l'effetto della concentrazione del templato sulla reazione RT e l'effetto della qualità del campione sui dati dopo la normalizzazione. La normalizzazione non contrasta l'effetto di saggi o campioni di bassa qualità (vedere Ottimizzazione e validazione del saggio).

Approcci di normalizzazione

In linea di massima, i metodi di normalizzazione contrastano la variabilità che può essere introdotta durante il processo a più fasi necessario per eseguire un'analisi qPCR (Figura 10.6). Tuttavia, l'applicazione della normalizzazione in una fase qualsiasi del processo può non controllare gli errori tecnici e/o i bias che sono stati o saranno introdotti in una fase precedente o successiva, rispettivamente. I metodi di normalizzazione non si escludono a vicenda e quindi si raccomanda di adottare una combinazione di controlli¹¹.

Figura 10.6. La qPCR è un processo a più fasi e ogni fase deve essere controllata. La normalizzazione deve essere considerata all'interno di una serie di controlli.

L'obiettivo della normalizzazione è quello di fornire un punto di riferimento stabile a cui riferire le misure; pertanto, la scelta del fattore di normalizzazione deve essere una misura stabile per tutta la durata dell'esperimento. Può trattarsi di uno o più geni di riferimento stabili o di una delle alternative, come il numero di cellule, la massa del tessuto, la concentrazione di RNA/DNA, uno spike esterno¹² o una misura rappresentativa dei geni espressi globalmente.

Selezione dei geni di riferimento

I geni di riferimento sono target la cui quantità non cambia in seguito all'esperimento. Quando si quantifica la variazione del numero di copie del DNA, in cui il numero di copie della sequenza di interesse può cambiare, la misurazione viene semplicemente normalizzata puntando a una regione genomica alternativa che è nota per non cambiare. Un esempio di applicazione di questo metodo è la misurazione dell'amplificazione genomica dell'Human Epidermal Growth Factor Receptor 2 (HER-2)¹³. L'instabilità genomica di HER-2 è un indicatore prognostico nel carcinoma mammario e la misurazione accurata dello stato di amplificazione di HER-2 è importante per la gestione delle pazienti. Lo stato di HER-2 può essere misurato mediante qPCR confrontando le copie di HER-2 con un altro target genomico che funge da controllo.

Quando si misura l'espressione genica, i geni di riferimento sono target con concentrazioni di mRNA che non cambiano in seguito all'esperimento. Un esempio di studio è quello in cui si misura l'effetto sull'espressione del gene X dopo l'aggiunta di un composto mitogeno a un monostrato di cellule. Per misurare la variazione del gene X è necessario un punto di riferimento, per cui si misura anche un altro gene (o più geni) che notoriamente non viene influenzato dal mitogeno in questione. In questo modo il ricercatore si trova di fronte alla sfida immediata di trovare un bersaglio di mRNA che non sia influenzato dalla procedura sperimentale, prima di poter studiare il GOI. Questo processo di validazione dei geni di riferimento è fondamentale per una misurazione accurata del GOI. L'approccio più diffuso alla normalizzazione consiste nell'ignorare questo processo e normalizzare i dati di espressione genica a un singolo gene di riferimento non validato. Questa pratica non è raccomandata ed è in diretta opposizione alle linee guida del MIQE¹. La quantificazione dell'mRNA mediante RT-qPCR è stata abitualmente compromessa dalla scelta errata dei geni di riferimento. Non è accettabile seguire la prassi relativamente comune di utilizzare un gene di riferimento perché i primer sono già nel congelatore, perché è stato usato storicamente su Northern blot, perché è stato usato da un collega o perché è stato usato in un altro laboratorio per un esperimento diverso. I geni di riferimento devono essere convalidati in scenari sperimentali specifici per avere la certezza che il gene di riferimento in questione non sia influenzato dall'esperimento. Se questa convalida non viene effettuata e il gene di riferimento viene influenzato dall'esperimento, i risultati potrebbero essere errati e le successive interpretazioni potrebbero risultare in dati privi di significato⁸.

Esiste una vasta letteratura scientifica che descrive diversi metodi di normalizzazione^7-14 così come una pletora di pubblicazioni che descrivono i protocolli necessari per identificare i geni normalizzatori più appropriati per un determinato scenario sperimentale. Mentre in passato la questione principale era se selezionare geni di riferimento singoli o multipli, la riduzione dei costi di gestione fa sì che le attuali best practice si siano spostate verso la misurazione di geni di riferimento multipli.

La selezione di geni di riferimento stabili richiede che l'analista valuti la stabilità della qPCR per un certo numero (di solito da 10 a 20 geni) di target di mRNA candidati⁷ su un sottoinsieme di campioni che rappresentano gli mRNA di test e di controllo. Un protocollo completo è fornito in Appendice A, Protocolli, di questa guida e può essere utilizzata in combinazione con diversi metodi analitici utilizzando programmi come REST¹⁵, GeNorm¹⁴, Bestkeeper¹⁶ o NormFinder¹⁷. Questa procedura è descritta più dettagliatamente nella sezione seguente, Analisi della stabilità del gene di riferimento.

Analisi della stabilità del gene di riferimento

Il gene di riferimento è letteralmente il perno dei saggi di quantificazione relativa qPCR. Per l'affidabilità dell'intero saggio è quindi fondamentale che il gene di riferimento sia stabile. Se l'espressione del gene di riferimento varia da un campione all'altro, la variazione si trasferisce direttamente ai risultati della quantificazione e la variabilità aggiunta può oscurare l'effetto biologico osservabile desiderato o, peggio ancora, può creare un effetto biologico del tutto artificiale, non correlato all'effettivo gene di interesse. Per questi motivi, si raccomanda vivamente di seguire diverse misure di sicurezza per rendere la variabilità del gene di riferimento insignificante e rendere le misure degli effetti biologici il più possibile significative.

La misura di sicurezza più importante è probabilmente quella di utilizzare non solo uno, ma due o più geni di riferimento. L'espressione di diversi geni di riferimento può essere mediata per ridurre la variabilità tecnica dovuta alla normalizzazione. Ciò può essere utile per migliorare la significatività delle misure di piccoli effetti biologici. Tuttavia, cosa ancora più importante, due o più geni di riferimento forniscono controlli reciproci per mantenere la stabilità e controllare gli eventi imprevisti che possono influenzare i livelli di espressione di uno dei geni di riferimento. Con un solo gene di riferimento, c'è il rischio che influenze inattese dell'espressione genica non vengano rilevate nel saggio.

Un'altra misura di sicurezza consiste nell'utilizzare più di un metodo per identificare i geni di riferimento stabili. Di seguito è riportato un esempio che illustra diversi aspetti della normalizzazione dei geni di riferimento, compreso un possibile vantaggio dell'uso di entrambi i metodi geNorm e NormFinder sullo stesso set di dati.

La tabella 10.3 contiene un elenco di candidati geni di riferimento che sono stati valutati durante un workshop che abbiamo precedentemente condotto con l'EMBL. I campioni sono stati raccolti da una coltura di cellule umane in due diversi gruppi di trattamento. Questo set di dati verrà utilizzato per dimostrare gli aspetti della validazione dei geni di riferimento.

Entrambi gli algoritmi NormFinder e geNorm sono stati sviluppati con l'ipotesi che il test di una moltitudine di candidati geni di riferimento possa essere utilizzato per classificare la stabilità dei singoli candidati geni di riferimento. L'ipotesi può essere vera se, ad esempio, tutti i candidati geni di riferimento variano in modo stocastico intorno a livelli di espressione stabili. Tuttavia, ciò potrebbe non essere necessariamente vero nella realtà. Per evitare risultati fuorvianti, è quindi prudente evitare i candidati geni di riferimento regolati e, in particolare, co-regolati.

Tabella 10.3Esempio di pannello di geni di riferimento per la convalida dei geni di riferimento. Per ottenere prestazioni accurate, è importante evitare i candidati geni di riferimento che sono co-regolati.

	Gene di riferimento	Numero di accesso.
1	18S	NR_03286
2	ACTB	NM_001101
3	ATP5B
4	B2M
5	CANX	NM_001024649
6	EIF4A2	NM_001967
7	CAPDHa	NM_002046
8	GAPDHb	NM_002046
9	NM_000181
10	PPIA	NM_021130
11	SDHA	NM_004168
12	TBP	NM_003194
13	TUBB	NM_178012
14	UBC	NM_021009
15	YWHAZ	NM_003406

L'elenco dei geni di riferimento candidati riportato nella Tabella 10.3 è stato scelto appositamente per selezionare geni che appartengono a classi funzionali diverse, riducendo la possibilità che i geni possano essere co-regolati. Un'eccezione degna di nota è rappresentata dalla GAPDH, presente in due versioni. Sebbene ciò non influisca sull'analisi, la prassi migliore è quella di evitare l'inserimento multiplo di geni che potrebbero essere sospettati di essere coregolati.

Il primo algoritmo ad essere dimostrato è geNorm. Questo algoritmo fornisce una valutazione della stabilità dei geni calcolando una misura di stabilità dei geni chiamata valore M, che si basa su confronti a coppie tra il candidato gene di riferimento analizzato e tutti gli altri candidati geni di riferimento nel set di dati. La procedura viene eseguita in modo iterativo, nel senso che in questo esempio viene prima eseguita su tutti i 15 candidati geni di riferimento, viene rimosso il meno stabile, il processo viene ripetuto sui 14 rimanenti, viene rimosso il secondo candidato meno stabile e così via fino a quando rimangono due geni di riferimento.

Ci possono essere momenti in cui l'identificazione del gene di riferimento più stabile può essere particolarmente impegnativa. Un caso può essere quello in cui tutti i candidati geni di riferimento hanno prestazioni scarse. Un altro caso può essere quello in cui tutti i candidati geni di riferimento hanno buone prestazioni. Per distinguere tra questi due casi, una linea guida utile è che i geni di riferimento con un valore M inferiore a 0,5 possono essere considerati espressi in modo stabile.

Il secondo algoritmo da dimostrare è NormFinder, che è un pacchetto di analisi dei geni di riferimento liberamente disponibile (Appendice B, Risorse aggiuntive). L'algoritmo sottostante adotta un approccio simile all'ANOVA per la valutazione della stabilità del gene di riferimento, in quanto l'intero gruppo e i sottogruppi vengono analizzati per le variazioni. Un vantaggio è che le misure ottenute sono direttamente correlate ai livelli di espressione genica. Una deviazione standard di 0,20 in unità C_q rappresenta quindi circa il 15% di variazione nei livelli di espressione del numero di copie del particolare gene di riferimento candidato.

Per comodità, in questa dimostrazione si accede a entrambi i pacchetti di analisi utilizzando il software di analisi dei dati GenEx (MultiD), ma sono disponibili anche come pacchetti indipendenti (Appendice B, Risorse aggiuntive).

I diagrammi a barre mostrati nella Figura 10.7 illustrano i geni di riferimento classificati in base alle rispettive misure di stabilità utilizzando entrambi gli algoritmi. Inoltre, un grafico che mostra la deviazione standard accumulata da NormFinder indica che una combinazione dei tre migliori geni di riferimento può produrre miglioramenti di stabilità.

Figura 10.7. Diagrammi a barre che mostrano le misure di stabilità: Valori M per geNorm e deviazioni standard per NormFinder. Inoltre, un grafico che mostra la deviazione standard accumulata da NormFinder indica che una combinazione dei tre migliori geni di riferimento può produrre miglioramenti della stabilità. Il set di dati è stato generato da saggi progettati per i candidati geni di riferimento indicati nella Tabella 10.3 e misurati su una coltura cellulare umana in due diversi gruppi di trattamento. Si noti che, in questo caso, gli algoritmi di stabilità del gene di riferimento geNorm e NormFinder non concordano sui migliori geni di riferimento.

Figura 10.8. Profilo di espressione medio centrato dei geni di riferimento candidati dei due campioni di ciascun gruppo di trattamento. I campioni 1 e 2 appartengono al primo gruppo di trattamento e i campioni 3 e 4 al secondo gruppo di trattamento. I profili di espressione di SDHA e CANX sono indicati in rosso. Il profilo di espressione di UBC è indicato in giallo. La tabella elenca i valori di Cq misurati nel set di dati.

A causa dei profili di espressione divergenti, è possibile che SDHA e CANX siano regolati dalle diverse alternative di trattamento e quindi non siano adatti come geni di riferimento. Rimuovendoli dal set di dati e ripetendo l'analisi, si ottiene un accordo tra entrambi gli algoritmi e la scelta migliore dei geni di riferimento è EIF4A2 e ATP53 (Figura 10.9). Nel calcolo di NormFinder delle deviazioni standard accumulate, è inoltre evidente che l'aggiunta di più geni di riferimento non migliora la stabilità.

Figura 10.9. L'ispezione dei profili di espressione e dei valori di Cq misurati (Figura 10.8) ha sollevato la preoccupazione che SDHA e CANX possano essere co-regolati nel saggio applicato. La coregolazione può disturbare gli algoritmi di stabilità del gene di riferimento. Diagrammi a barre che mostrano le misure di stabilità: A) valori M per geNorm e B) deviazioni standard per NormFinder. Il set di dati è lo stesso utilizzato nella Figura 10.8, tranne per il fatto che i dati relativi a SDHA e CANX sono stati rimossi. Si noti che con questo set di dati ridotto gli algoritmi di stabilità dei geni di riferimento geNorm e NormFinder concordano sui migliori geni di riferimento.

L'analisi dei dati in questo esempio serve a illustrare che l'uso di geNorm e NormFinder in parallelo permette di identificare i candidati geni di riferimento co-regolati e che la rimozione di questi geni da ulteriori studi fornisce un'identificazione finale di geni di riferimento che può essere adottata con maggiore sicurezza rispetto all'uso di una singola analisi. L'identificazione e la selezione di geni di riferimento stabili porta a una maggiore sicurezza nell'analisi dei dati.

Metodi di normalizzazione alternativi

Sebbene la normalizzazione ai geni di riferimento sia il metodo più comune per la normalizzazione dei saggi, ci sono situazioni in cui questo approccio non è adatto, ad esempio quando si deve confrontare un gran numero di geni in un gruppo eterogeneo di campioni o quando si profila il miRNA. In questi scenari è necessario adottare una strategia alternativa.

Normalizzazione rispetto alla massa del tessuto o al numero di cellule

La misurazione del numero di cellule o della massa del tessuto da utilizzare come fattore di normalizzazione non è così semplice come potrebbe sembrare a prima vista. Gli esperimenti di coltura cellulare sono relativamente facili da normalizzare in base al numero di cellule. Tuttavia, l'aggiunta di un trattamento potrebbe avere un impatto sulla morfologia cellulare, complicando il rapporto tra numero di cellule e RNA/geni totali espressi rispetto a una coltura di controllo. Il trattamento sperimentale può comportare la produzione di matrice extracellulare, causando differenze nell'efficienza di estrazione degli acidi nucleici.

I tessuti biologici possono essere altamente eterogenei all'interno di un soggetto e tra soggetti diversi, con maggiori variazioni evidenti quando il tessuto sano viene confrontato con quello malato. Anche tessuti apparentemente meno complessi, come il sangue, possono differire notevolmente nel numero e nella composizione delle cellule, tanto che l'espressione genica varia notevolmente tra donatori apparentemente sani¹⁸.

Qualsiasi ritardo nei processi utilizzati per purificare l'acido nucleico comporterà alterazioni nell'RNA misurato. Ad esempio, i ritardi nel trattamento delle cellule mononucleari del sangue periferico e nell'estrazione dell'RNA dalle cellule comportano notevoli cambiamenti nell'espressione genica¹⁹. Anche i metodi alla base delle procedure di estrazione sono fonti importanti di variazione tecnica. Anche il processo di isolamento scelto per il campionamento delle cellule derivate dal sangue e la purificazione dell'RNA comportano differenze nei profili apparenti di espressione genica²⁰. Pertanto, la prima considerazione sulla normalizzazione consiste nell'assicurare che la raccolta e il trattamento siano assolutamente identici per tutti i campioni. È quindi fondamentale eseguire un controllo di qualità sufficiente per essere certi della concentrazione, dell'integrità e della purezza del campione (Purificazione del campione e valutazione della qualità e i protocolli associati in Appendice A).

Normalizzazione alla concentrazione di RNA

Come minimo, è importante una stima della concentrazione del templato (DNA per la qPCR o RNA per la RT-qPCR) e, come menzionato nell& nbsp;Purificazione del campione e valutazione della qualità, è fondamentale assicurarsi che venga utilizzato lo stesso strumento per tutte le misurazioni, poiché anche la determinazione della concentrazione di acido nucleico è variabile e dipendente dalla tecnica.

Quando si misura la concentrazione di RNA totale, la stragrande maggioranza del campione è composta da rRNA, mentre solo una piccola frazione è costituita dall'mRNA di interesse quando si esamina l'espressione genica o dall'sncRNA quando si esamina la regolazione dell'espressione genica. Ciò significa che se la concentrazione di rRNA aumenta di poco ma l'mRNA rimane costante, la concentrazione di RNA totale aumenterà. La concentrazione di mRNA deve aumentare in misura significativa per causare un aumento apparente della concentrazione di RNA totale. Pertanto, la concentrazione di rRNA è una misura inaffidabile della concentrazione di mRNA, ma per molti protocolli è necessaria un'uguale concentrazione di RNA per garantire una trascrizione inversa accurata (vedere Trascrizione inversa).

Normalizzazione all'espressione genica globale

Quando si misura un gran numero di target, l'analista può stimare la media globale dell'espressione genica totale e identificare le sequenze di RNA regolate che si discostano da questa media. Questo approccio è convenzionalmente utilizzato per la normalizzazione degli array di espressione genica. È una valida alternativa all'uso di geni di riferimento e può essere preferibile quando si misurano molti target.

Un altro approccio recentemente esplorato è la misurazione degli elementi ripetuti endogenamente espressi (ERE) che sono presenti in molti mRNA. Molte specie contengono questi elementi ripetuti (ALU nei primati, elementi B nei topi), che possono fornire una stima della frazione di mRNA. È stato dimostrato che la misurazione di queste sequenze target funziona come i sistemi di normalizzazione convenzionali⁹  (Le Bert, et al., in preparazione) e può offrire una soluzione universale o un'alternativa per esperimenti complessi in cui non sono disponibili combinazioni di geni di riferimento stabili.

Normalizzazione dei dati sui miRNA

Ad oggi non è stato riportato un gene di riferimento universale per i miRNA. Pertanto, la scelta del sistema di normalizzazione è ancora piuttosto empirica. Quando è possibile, i miRNA invarianti stabili possono essere identificati da approcci a livello di genoma, ad esempio i microarray. Anche i piccoli RNA nucleolari (snoRNA) sono stati utilizzati come geni di riferimento. Anche l'espressione genica globale è un metodo utile per normalizzare l'espressione dei miRNA quando non si conosce un riferimento stabile e sono state analizzate diverse centinaia di target^21,22,23. Questo metodo è più appropriato per chi utilizza approcci che comportano la cattura di tutti i miRNA come cDNA in forma multiplexata, ad es, Exiqon e miQPCR (si veda Castoldi et al. in PCR Technologies, Current Innovations²⁴).

Ripetizioni biologiche e tecniche

Lo scopo della normalizzazione è quello di evitare errori sistematici e ridurre la variabilità dei dati per l'eventuale analisi statistica. Un altro aspetto importante dell'impostazione dei dati per l'analisi statistica è l'uso di repliche dei dati.

Le repliche biologiche sono assolutamente necessarie per l'analisi statistica. I livelli di significatività statistica sono spesso fissati a un cut-off di significatività del 5%. Per effetti biologici vicini a tale livello di significatività, può essere necessario disporre di almeno 20 repliche biologiche per determinare il livello di significatività del saggio (1:20 corrispondente al 5%). In realtà, è stato suggerito che per una stima accurata della significatività è necessario registrare un numero di osservazioni almeno 50 volte superiore²⁵, cioè dell'ordine di un migliaio di campioni biologici. Naturalmente, le limitazioni pratiche raramente consentono di effettuare repliche biologiche a questi livelli. Inoltre, le stime accurate del numero di repliche biologiche necessarie per soddisfare un determinato livello di significatività dipendono anche dal livello di variabilità dei dati. Tuttavia, è importante rendersi conto che un errore comune è quello di sottostimare il numero necessario di repliche biologiche per poter giungere a conclusioni affidabili. Si raccomanda di eseguire uno studio pilota iniziale per valutare la variabilità intrinseca del saggio e la dimensione potenziale dell'effetto biologico osservabile, al fine di disporre di una buona base per stimare il numero necessario di repliche biologiche²⁶.

Le repliche tecniche non vengono utilizzate direttamente per l'analisi statistica. Invece, le repliche tecniche sono utilizzate per il backup dei campioni (nel caso in cui alcuni campioni vadano persi nel processo di manipolazione tecnica) e per migliorare la valutazione dell'accuratezza dei dati. Le repliche tecniche possono migliorare l'accuratezza dei dati se è vera l'ipotesi che variano stocasticamente intorno alla misura accurata in ogni fase del processo di manipolazione tecnica. La media delle repliche tecniche è più vicina alla misura accurata. L'effetto della media delle repliche tecniche può essere illustrato osservando l'ampiezza dell'intervallo di confidenza in una serie di dati simulati con una variabilità predeterminata, ossia una deviazione standard fissata a uno. Come si vede nella Tabella 10.4, l'intervallo di confidenza si riduce con l'aumentare del numero di repliche tecniche (campioni), indicando una stima più precisa della misura accurata. Inoltre, il restringimento dell'intervallo di confidenza è più evidente al basso numero di repliche tecniche. Aumentando il numero di repliche da 2-3 si riduce l'intervallo di confidenza da 8,99 a 2,48, ossia un miglioramento di oltre 3 volte della precisione nella stima della misura accurata. Sebbene ulteriori repliche continuino a migliorare la stima dell'accuratezza della misura, l'effetto è di entità decrescente. Pertanto, è evidente che nei casi in cui la variabilità della manipolazione tecnica è un problema, può essere un grande vantaggio utilizzare triplicati piuttosto che duplicati.

Tabella 10.4Dimensione degli intervalli di confidenza delle medie stimate normalizzate a una deviazione standard di 1 e a un livello di confidenza α del 5%. L'intervallo di confidenza diventa più piccolo con l'aumentare del numero di campioni tecnici replicati, indicando una stima più precisa della misura accurata con un numero maggiore di campioni replicati.

Intervalli di confidenza delle medie stimate
Campioni	Cl (α=0.05 e SD=1)
2	8.99
3	2.48
4	1.59
5	1.24
10	0.72
20	0.47
50	0,28

Le repliche tecniche possono essere raccolte in diverse fasi del processo di trattamento dei campioni, tra cui l'estrazione dell'RNA, la trascrizione inversa e la rilevazione qPCR. Se si rilevano repliche tecniche in diverse fasi, si genera un disegno sperimentale annidato. Uno studio pilota che sfrutti un disegno sperimentale annidato può aiutare a identificare le fasi di manipolazione dei campioni che contribuiscono maggiormente agli errori tecnici di manipolazione e, sulla base di queste informazioni, è possibile calcolare un piano di campionamento ottimale²⁷.

Analisi statistica e visualizzazione dei dati

L'analisi scientifica dei dati biologici si basa sulla formulazione e sulla verifica di ipotesi. La formulazione di un'ipotesi richiede una comprensione dettagliata delle condizioni e delle variabili del saggio. Il successo della verifica di un'ipotesi implica un'esecuzione attenta e un disegno sperimentale appropriato per massimizzare il segnale osservabile desiderato, riducendo al minimo la variabilità tecnica. In questo contesto, è utile distinguere tra studi esplorativi e di conferma (Figura 10.10).

Figura 10.10. Diagramma di flusso che illustra le operazioni coinvolte nelle analisi statistiche esplorative e di conferma. Il lato sinistro della figura, prima della freccia tratteggiata, mostra le operazioni di uno studio statistico esplorativo. Il lato destro della figura, dopo la freccia tratteggiata, mostra le operazioni di uno studio statistico di conferma.

Lo scopo dello studio esplorativo è quello di analizzare i dati con una o più tecniche diverse per avvalorare un'ipotesi. L'insieme dei dati può essere ridefinito e/o possono essere impiegate ripetutamente diverse tecniche di analisi per sostenere una o più ipotesi. Lo studio esplorativo è quindi molto flessibile alle specificità di qualsiasi domanda scientifica. Tuttavia, il ripetersi di test di ipotesi su una serie di dati può portare a problemi che minano le conclusioni statistiche. Ciò è dovuto ai test multipli, che si riferiscono al fatto che un test statistico con diverse ipotesi indipendenti ha maggiori probabilità di produrre una significatività positiva e che le probabilità di questo aumentano man mano che vengono testate altre ipotesi, anche se le distribuzioni di probabilità sottostanti sono identiche. Per evitare risultati statistici fuorvianti, lo studio esplorativo viene quindi spesso combinato con uno studio di conferma.

I requisiti per uno studio di conferma si basano su criteri statistici molto più severi. In primo luogo, l'ipotesi di studio, compresi i criteri di significatività, deve essere definita prima della raccolta dei dati e prima dell'analisi. Inoltre, la serie di dati da analizzare deve essere stata raccolta esclusivamente per questo scopo. È statisticamente scorretto riutilizzare la serie di dati dello studio esplorativo nello studio di conferma, poiché tale serie di dati favorirebbe intrinsecamente l'ipotesi proposta. Il risultato finale dello studio di conferma è un'ipotesi respinta o accettata secondo i criteri prestabiliti.

Test statistici

Per i test statistici, si analizza la probabilità che un fenomeno osservato si sia verificato per caso. Questa è chiamata ipotesi nulla²⁸. Se il fenomeno osservato è raro secondo l'ipotesi nulla, la conclusione è che è improbabile che l'ipotesi nulla sia valida. L'ipotesi nulla viene rifiutata e viene accettata la probabilità che l'ipotesi alternativa sia significativa.

La probabilità stimata che il fenomeno osservato si sia verificato per caso è chiamata valore p. Il valore p è misurato in un intervallo da 0 a 1, o equivalentemente, in unità percentuali. I criteri statistici per uno studio di conferma includono un cut-off alfa al di sotto del quale i valori calcolati di p indicherebbero la significatività del fenomeno osservato. Comunemente si usa un cut-off alfa del 5%, anche se questo deve essere aggiustato per adattarsi ai criteri desiderati e necessari che sono specifici per l'oggetto di studio.

Sono stati sviluppati molti algoritmi per calcolare i valori di p sotto varie ipotesi e per diversi scopi. Un algoritmo comune è il test t di Student. Il test t di Student viene utilizzato per calcolare un valore p basato sulla differenza dei valori medi tra due gruppi di dati. L'ipotesi principale del test t di Student è che i due gruppi di dati siano indipendenti e conformi a distribuzioni normali. Un vantaggio del test t di Student è che è potente, rispetto ai test statistici non parametrici²⁹. Un test non parametrico equivalente al test t di Student può essere uno dei test statistici non parametrici più noti: il test della somma di rango di Wilcoxon (talvolta chiamato test U di Mann-Whitney; da non confondere con il test di rango firmato di Wilcoxon, utilizzato per confrontare due gruppi appaiati). I test statistici non parametrici, come il Wilcoxon rank-sum test, hanno un vantaggio rispetto ai test statistici parametrici, come il t-test di Student, in quanto non dipendono da ipotesi preliminari sulle distribuzioni dei dati. Il test di Kolmogorov-Smirnov per la distribuzione normale può essere utilizzato per decidere se applicare il test t di Student o uno dei test non parametrici.nbsp;p calcolo del valore, gli insiemi di dati che vengono immessi nell'algoritmo di calcolo del valore di p possono essere manipolati per facilitare l'osservazione delle proprietà desiderate nell'insieme di dati. La combinazione delle fasi di manipolazione dei dati grezzi e della scelta dell'algoritmo di calcolo del valore p fa parte della costruzione di un modello di ipotesi.

C'è un alto livello di libertà nella costruzione di modelli di ipotesi nella fase esplorativa di un'analisi statistica e questa è una parte importante dell'indagine scientifica. Tuttavia, un'ipotesi non viene mai dimostrata utilizzando un approccio scientifico e statistico. Un approccio scientifico corretto consiste nel formulare un'ipotesi nulla, utilizzare una serie di dati indipendenti (preferibilmente raccolti di recente) e accettare o rifiutare l'ipotesi nulla secondo il diagramma di flusso dello studio confermativo (Figura 10.10).

Tecniche di visualizzazione per l'analisi univariata

Come esistono molti metodi di analisi, esistono anche molte tecniche di visualizzazione dei dati tra cui scegliere. Per l'analisi dei dati univariati, un semplice diagramma a barre con barre di errore associate è una tecnica di visualizzazione appropriata. Anche se si tratta di una tecnica di visualizzazione comune e semplice, ci sono aspetti che vale la pena sottolineare. In primo luogo, le barre di errore possono illustrare diverse fonti di variabilità: la variabilità intrinseca dei dati (la deviazione standard, SD) o la precisione con cui è stato determinato il valore medio. In secondo luogo, la precisione con cui è stato determinato il valore medio può essere illustrata in modi diversi, ma in ultima analisi dipende da una combinazione della variabilità intrinseca dei dati insieme al numero di campioni (N) e, nella sua forma grezza, è chiamata errore standard della media (SEM, equazione 1):

Equazione 1. SEM

Tuttavia, il SEM non è una misura molto intuitiva e non è semplice confrontare i SEM di esperimenti diversi in modo significativo. Un modo più popolare di illustrare la precisione della media stimata e di indicare la significatività statistica in modo grafico è l'intervallo di confidenza (CI, Equazione 2):

Equazione 10-2. Cl

La presenza del SEM può essere riconosciuta nell'equazione per l'intervallo di confidenza come il rapporto tra la deviazione standard (SD) e la radice quadrata del numero di campioni (N) e quindi è evidente che l'intervallo di confidenza si basa sul SEM. Il limite inferiore dell'intervallo di confidenza è costruito sottraendo alla media il SEM moltiplicato per un percentile di una distribuzione t. Il limite superiore dell'intervallo di confidenza è costituito dal rapporto tra la deviazione standard (SD) e la radice quadrata del numero di campioni (N). Il limite superiore dell'intervallo di confidenza è costruito aggiungendo il SEM moltiplicato per un percentile di una distribuzione t dalla media. Il livello di confidenza dell'intervallo di confidenza è fissato dal livello di confidenza associato al valore critico t*; in genere un livello di confidenza del 95%.

La figura 10.11 mostra un grafico a barre con barre di errore che denotano l'intervallo di confidenza del 95% all'interno di ciascun gruppo sperimentale, evidenziando l'incertezza associata alla stima media per un esempio di espressione genica in campioni provenienti da diversi organi dopo il trattamento con diverse dosi di farmaco. Inoltre, vengono mostrati i valori di significatività statistica del t-test p per la differenza nell'espressione genica tra i campioni di controllo e ciascuno dei tre diversi campioni provenienti da risposte a diverse dosi di farmaco, indicati con una notazione asterisco. È consuetudine che un asterisco corrisponda a un valore p inferiore a 0,05, due asterischi corrispondano a un valore p inferiore a 0,01 e tre asterischi corrispondano a un valore p inferiore a 0,001.

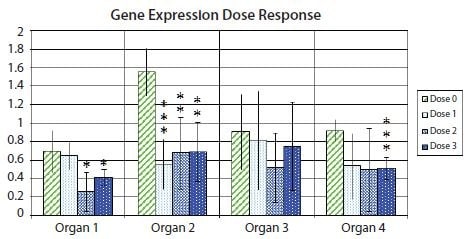
Figura 10.11. Variazione di ripiegamento (log2) dell'espressione di un gene di interesse rispetto a una coppia di geni di riferimento, relativamente all'espressione nel campione con l'espressione più bassa all'interno di ciascun tipo di organo. Le altezze delle barre indicano l'espressione media del gene in diversi campioni in gruppi di campioni non trattati (dose 0) o trattati a una delle tre diverse dosi di farmaco (dose 1, dose 2 e dose 3). Le barre di errore indicano le stime degli intervalli di confidenza al 95% delle espressioni medie. Un asterisco indica una differenza statisticamente significativa tra le medie di un gruppo di campioni trattati rispetto alla media del gruppo di campioni non trattati al 5%; due asterischi indicano una differenza statisticamente significativa all'1%; tre asterischi indicano una differenza statisticamente significativa allo 0,1%.

Dato che la notazione con l'asterisco nasconde il valore assoluto di p, è spesso incoraggiato includere una tabella con i valori assoluti di p, come mostrato nell'esempio della Tabella 10.5. Uno dei motivi è che un valore di p, ad esempio, di 0,032 è solo leggermente più "significativo" di un p valore di 0,055. Casi limite come questo possono generare una certa confusione nel decidere quale cut-off utilizzare per classificare i dati come significativi. In casi realistici, un pvalore di 0,051 potrebbe essere altrettanto significativo di un p valore di 0,049, eppure un cut-off rigoroso (anche se fondamentalmente arbitrario) di 0,05 classificherebbe l'uno come significativo e l'altro no.

Tabella 10.5Stime di significatività della differenza delle medie. Le medie dell'espressione di un gene di interesse di un set di campioni trattati vengono confrontate con le medie dei campioni non trattati ed espresse rispetto ai dati di espressione di due geni di riferimento. I dati sono presentati rispetto al campione con l'espressione più bassa per ciascun tipo di organo (dati mostrati nella Figura 10.12). Per produrre i valori di p è stato utilizzato il test t di Student.

Espressione genica valori p
	Organo 1	Organo 2	Organo 3	Organo 4
Dose 1 vs Dose 0	0.70274	0.00034***	0,78194	0.05551
Dose 2 vs Dose 0	0.01379*	0,00295**	0.20956	0.07582
Dose 3 vs Dose 0	0.03180*	0,00157**	0.61582	0,00075***

Esiste tuttavia una variante della visualizzazione del diagramma a barre che sfrutta l'intervallo di confidenza della differenza tra le medie per evitare molti, se non tutti, gli svantaggi dei diagrammi a barre tradizionali²⁴. Con l'intervallo di confidenza della differenza tra le medie, è possibile stimare direttamente la significatività statistica con le barre di errore associate, evidenziando allo stesso tempo la dimensione dell'effetto biologico e la variabilità dei dati. La Figura 10.12 mostra la variante con l'intervallo di confidenza della differenza tra le medie dei dati utilizzati nella Figura 10.11. Si noti che gli intervalli di confidenza che non comprendono la differenza zero tra le medie corrispondono a risultati significativi al livello di confidenza corrispondente al valore di cut-off p (5% in Figura 10.11 e Tabella 10.5).

Figura 10.12. Diagramma a barre che mostra la differenza tra le medie del set di campioni non trattati (Dose 0) e uno dei set di campioni trattati (Dose 1, Dose 2 o Dose 3) nel set di dati della Figura 10.11. Le barre di errore mostrano l'intervallo di confidenza della differenza tra le medie. Le barre di errore che non attraversano l'asse delle ascisse indicano che il confronto tra le medie corrispondenti è statisticamente significativo al 5% in un t-test. Tecnologia PCR, innovazioni attuali-3a ed. di Taylor and Francis Group LLC Books. Riprodotto con il permesso di Taylor and Francis Group LLC Books nel formato di riutilizzo in un libro/e-book tramite il Copyright Clearance Center.

I dati multivariati sono dati raccolti su più variabili per ogni unità di campionamento. I dati utilizzati nelle Figure 10.11 e 10.12 sono multivariati in quanto dipendono da variabili come la dose e il tipo di organo. Tuttavia, le analisi statistiche nelle figure 10.11 e 10.12 sono comunque univariate, in quanto ogni rappresentazione (barra) illustra solo una variabile, l'espressione genica, rispetto a misure fisse delle altre variabili. Per le tecniche di analisi dei dati multivariati, il clustering gerarchico e l'analisi delle componenti principali sono buone opzioni per la rappresentazione dei dati.

Hierarchical Clustering

Uno dei metodi più semplici e utili per caratterizzare i dati è quello di tracciare i dati in un diagramma di dispersione (ad esempio, tracciare le misure di C_q di un gene rispetto ai corrispondenti valori C_q di un altro gene per un insieme di campioni biologici in un grafico 2D). I grafici in una o due dimensioni sono facilmente visualizzabili dagli occhi umani. Con gli strumenti appropriati è possibile ottenere anche grafici in tre dimensioni, ma i grafici di dimensioni più elevate sono molto più difficili da visualizzare. Tuttavia, per gli studi esplorativi, il set di dati è intrinsecamente multidimensionale e i grafici di dispersione di interi set di dati possono diventare poco pratici. In un set di dati qPCR, possono essere rappresentati, ad esempio, diversi geni e/o diversi tipi di campioni biologici.

Un modo alternativo e popolare di caratterizzare e visualizzare i dati di studi esplorativi consiste nell'analizzare le misure di distanza tra i punti di dati nel diagramma di dispersione. Esistono diverse misure di distanza, tra cui le correlazioni euclidee, di Manhattan e di Pearson. Grazie alla potenza di calcolo, è facile calcolare le distanze, anche per i dati multidimensionali con una dimensionalità molto più elevata rispetto alle tre dimensioni. Per il clustering gerarchico agglomerativo, viene eseguito il seguente processo iterativo: 1) Trovare i due oggetti più vicini e unirli in un cluster; 2) Definire il nuovo cluster come un nuovo oggetto attraverso un metodo di clustering; 3) Ripetere da 1) fino a quando tutti gli oggetti sono stati combinati in cluster³⁰. Le alternative per i metodi di clustering includono il metodo di Ward, Single linkage e Average linkage³¹. Un dendrogramma è spesso usato per visualizzare i risultati del clustering gerarchico.

L'interpretazione dei dendrogrammi del clustering gerarchico dei dati qPCR spesso porta a conclusioni sulle somiglianze dei profili di espressione genica. In uno studio esplorativo, queste somiglianze possono essere utilizzate per formulare ipotesi sulla coregolazione dell'espressione genica, che possono essere accettate o respinte in successivi studi di conferma. I vantaggi dei dendrogrammi di clustering gerarchico includono la chiarezza con cui vengono visualizzate le relazioni di similarità. D'altra parte, la forte enfasi sulle misure di somiglianza può essere percepita come limitante rispetto alla formulazione di ipotesi, poiché profili di espressione simili possono essere attributi ridondanti nelle ipotesi. Potrebbe essere più utile identificare insiemi di profili di espressione che si completano a vicenda in una combinazione specifica, per rispondere all'ipotesi desiderata.

Analisi delle componenti principali

Un altro modo alternativo e popolare per caratterizzare e visualizzare i dati provenienti da studi esplorativi è quello di sfruttare le informazioni contenute nell'intero set di dati multidimensionali, selezionare le proprietà desiderate e proiettarle su un grafico a dispersione di dimensioni inferiori, come un grafico 2D o 3D. Ciò può essere ottenuto utilizzando l'analisi delle componenti principali (PCA)^{32,33,34, 35}. In questo caso, il sistema di coordinate originale del set di dati (cioè i profili di espressione misurati mediante qPCR) viene trasformato in un nuovo spazio multidimensionale in cui vengono costruite nuove variabili (componenti principali: PC o fattori). Ogni PC è una combinazione lineare dei soggetti del set di dati originale. Per definizione matematica, le PC vengono estratte in ordine successivo di importanza. Ciò significa che la prima PC spiega la maggior parte dell'informazione (varianza) presente nei dati, la seconda meno e così via. Pertanto, le prime due o tre coordinate delle PC (chiamate punteggi) possono essere utilizzate per ottenere una proiezione dell'intero set di dati su una dimensione convenientemente piccola, adatta alla visualizzazione in un grafico 2D o 3D. Utilizzando le prime due o tre PC per la rappresentazione, si ottiene la proiezione che tiene conto della maggiore variabilità del set di dati. La varianza derivante dalle condizioni di progettazione sperimentale dovrebbe essere sistematica, mentre la varianza di confondimento dovrebbe essere casuale, quindi questa rappresentazione può essere desiderata in condizioni appropriate.

Come già notato in precedenza per il clustering gerarchico, l'interpretazione della PCA della qPCR spesso porta a conclusioni sulle somiglianze dei profili di espressione genica. Sebbene la PCA e il clustering gerarchico possano fornire approfondimenti complementari sui modelli di coregolazione dell'espressione genica, entrambe le tecniche si concentrano sulle somiglianze dei profili di espressione genica. Ciò limita i tipi di ipotesi che possono essere trovate in studi esplorativi che utilizzano solo queste tecniche. Per ampliare la portata delle ipotesi generate negli studi esplorativi, è stato recentemente proposto un approccio all'analisi multivariata guidato dalle ipotesi²⁴. Algoritmi guidati da ipotesi e progettati su misura possono identificare ipotesi biologicamente rilevanti che altrimenti potrebbero sfuggire alle tecniche comunemente utilizzate per l'analisi multivariata dei dati.

I materiali

Si è verificato un errore inatteso.

Response not successful: Received status code 500

1. Bustin SA, Benes V, Garson JA, Hellemans J, Huggett J, Kubista M, Mueller R, Nolan T, Pfaffl MW, Shipley GL, et al. 2009. The MIQE Guidelines: Minimum Information for Publication of Quantitative Real-Time PCR Experiments. 55(4):611-622. https://doi.org/10.1373/clinchem.2008.112797

2. Guescini M, Sisti D, Rocchi MB, Stocchi L, Stocchi V. 2008. A new real-time PCR method to overcome significant quantitative inaccuracy due to slight amplification inhibition. BMC Bioinformatics. 9(1): https://doi.org/10.1186/1471-2105-9-326

3. Rutledge RG, Stewart D. 2008. Critical evaluation of methods used to determine amplification efficiency refutes the exponential character of real-time PCR. BMC Mol Biol. 9(1):96. https://doi.org/10.1186/1471-2199-9-96

4. Rutledge RG, Stewart D. 2008. A kinetic-based sigmoidal model for the polymerase chain reaction and its application to high-capacity absolute quantitative real-time PCR. BMC Biotechnology. 8(1):47. https://doi.org/10.1186/1472-6750-8-47

5. Livak KJ, Schmittgen TD. 2001. Analysis of Relative Gene Expression Data Using Real-Time Quantitative PCR and the 2???CT Method. Methods. 25(4):402-408. https://doi.org/10.1006/meth.2001.1262

6. Pfaffl MW. 2001. A new mathematical model for relative quantification in real-time RT-PCR. 29(9):45e-45. https://doi.org/10.1093/nar/29.9.e45

7. Dheda K, Huggett JF, Bustin SA, Johnson MA, Rook G, Zumla A. 2004. Validation of housekeeping genes for normalizing RNA expression in real-time PCR. BioTechniques. 37(1):112-119. https://doi.org/10.2144/04371rr03

8. Dheda K, Huggett J, Chang J, Kim L, Bustin S, Johnson M, Rook G, Zumla A. 2005. The implications of using an inappropriate reference gene for real-time reverse transcription PCR data normalization. Analytical Biochemistry. 344(1):141-143. https://doi.org/10.1016/j.ab.2005.05.022

9. Vermeulen J, De Preter K, Lefever S, Nuytens J, De Vloed F, Derveaux S, Hellemans J, Speleman F, Vandesompele J. 2011. Measurable impact of RNA quality on gene expression results from quantitative PCR. 39(9):e63-e63. https://doi.org/10.1093/nar/gkr065

10. Ibberson D, Benes V, Muckenthaler MU, Castoldi M. 2009. RNA degradation compromises the reliability of microRNA expression profiling. BMC Biotechnology. 9(1):102. https://doi.org/10.1186/1472-6750-9-102

11. Huggett J, Dheda K, Bustin S, Zumla A. 2005. Real-time RT-PCR normalisation; strategies and considerations. Genes Immun. 6(4):279-284. https://doi.org/10.1038/sj.gene.6364190

12. Mitsuhashi M, Tomozawa S, Endo K, Shinagawa A. 2006. Quantification of mRNA in Whole Blood by Assessing Recovery of RNA and Efficiency of cDNA Synthesis. 52(4):634-642. https://doi.org/10.1373/clinchem.2005.048983

13. Whale AS, Huggett JF, Cowen S, Speirs V, Shaw J, Ellison S, Foy CA, Scott DJ. 2012. Comparison of microfluidic digital PCR and conventional quantitative PCR for measuring copy number variation. 40(11):e82-e82. https://doi.org/10.1093/nar/gks203

14. Vandesompele J, De Preter K, Pattyn F, Poppe B, Van Roy N, De Paepe A, Speleman F. 2002. Genome Biol. 3(7):research0034.1. https://doi.org/10.1186/gb-2002-3-7-research0034

15. Pfaffl MW. 2002. Relative expression software tool (REST(C)) for group-wise comparison and statistical analysis of relative expression results in real-time PCR. 30(9):36e-36. https://doi.org/10.1093/nar/30.9.e36

16. Pfaffl MW, Tichopad A, Prgomet C, Neuvians TP. 2004. Determination of stable housekeeping genes, differentially regulated target genes and sample integrity: BestKeeper ? Excel-based tool using pair-wise correlations. Biotechnology Letters. 26(6):509-515. https://doi.org/10.1023/b:bile.0000019559.84305.47

17. Andersen CL, Jensen JL, Ørntoft TF. 2004. Normalization of Real-Time Quantitative Reverse Transcription-PCR Data: A Model-Based Variance Estimation Approach to Identify Genes Suited for Normalization, Applied to Bladder and Colon Cancer Data Sets. Cancer Res. 64(15):5245-5250. https://doi.org/10.1158/0008-5472.can-04-0496

18. Eady JJ, Wortley GM, Wormstone YM, Hughes JC, Astley SB, Foxall RJ, Doleman JF, Elliott RM. 2005. Variation in gene expression profiles of peripheral blood mononuclear cells from healthy volunteers. Physiological Genomics. 22(3):402-411. https://doi.org/10.1152/physiolgenomics.00080.2005

19. Barnes MG, Grom AA, Griffin TA, Colbert RA, Thompson SD. 2010. Gene Expression Profiles from Peripheral Blood Mononuclear Cells Are Sensitive to Short Processing Delays. Biopreservation and Biobanking. 8(3):153-162. https://doi.org/10.1089/bio.2010.0009

20. Debey S, Schoenbeck U, Hellmich M, Gathof BS, Pillai R, Zander T, Schultze JL. 2004. Comparison of different isolation techniques prior gene expression profiling of blood derived cells: impact on physiological responses, on overall expression and the role of different cell types. Pharmacogenomics J. 4(3):193-207. https://doi.org/10.1038/sj.tpj.6500240

21. Mestdagh P, Van Vlierberghe P, De Weer A, Muth D, Westermann F, Speleman F, Vandesompele J. 2009. A novel and universal method for microRNA RT-qPCR data normalization. Genome Biol. 10(6):R64. https://doi.org/10.1186/gb-2009-10-6-r64

22. Mestdagh P, Derveaux S, Vandesompele J. 2012. Whole-Genome RT-qPCR MicroRNA Expression Profiling.121-130. https://doi.org/10.1007/978-1-61779-424-7_10

23. D?haene B, Mestdagh P, Hellemans J, Vandesompele J. 2012. miRNA Expression Profiling: From Reference Genes to Global Mean Normalization.261-272. https://doi.org/10.1007/978-1-61779-427-8_18

24. Nolan T, Bustin SA. 2013. PCR Technology: Current Innovations. 3. CRC Press.

25. Manly B. 1998. Randomization, Bootstrap and Monte Carlo Methods.. 2. Chapman Hall:

26. Kitchen RR, Kubista M, Tichopad A. 2010. Statistical aspects of quantitative real-time PCR experiment design. Methods. 50(4):231-236. https://doi.org/10.1016/j.ymeth.2010.01.025

27. Tichopad A, Kitchen R, Riedmaier I, Becker C, Sta?hlberg A, Kubista M. 2009. Design and Optimization of Reverse-Transcription Quantitative PCR Experiments. 55(10):1816-1823. https://doi.org/10.1373/clinchem.2009.126201

28. Fisher R. 1966. The design of experiments.. 8. Hafner: Edinburgh:

29. Motulsky H. 1995. Intuitive Biostatistics. New York: Oxford University Press.

30. Ward JH. 1963. Hierarchical Grouping to Optimize an Objective Function. Journal of the American Statistical Association. 58(301):236-244. https://doi.org/10.1080/01621459.1963.10500845

31. Lance GN, Williams WT. 1967. A General Theory of Classificatory Sorting Strategies: 1. Hierarchical Systems. The Computer Journal. 9(4):373-380. https://doi.org/10.1093/comjnl/9.4.373

32. Rao C. 1964. The use and interpretation of principal components analysis in applied research..

33. Hotelling H. 1933. Analysis of a complex of statistical variables into principal components.. Journal of Educational Psychology. 24(6):417-441. https://doi.org/10.1037/h0071325

34. Pearson K. 1901. LIII. On lines and planes of closest fit to systems of points in space. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 2(11):559-572. https://doi.org/10.1080/14786440109462720